해시 테이블

Direct Access Table

배열의 인덱스 접근의 시간복잡도는 O(1)이었다.

인덱스는 데이터의 순서에 해당하는 색인, 데이터이다.

 

이 인덱스를 순서가 아닌 Key라 생각하고 데이터를 저장할 수 있는데 이러한 방식으로 데이터를 저장하고 관리하는 테이블을 Direct Access Table 이라 한다.

Key (= 인덱스)라고 생각하고 value에 접근하는 방식이다.

 

특징

효율적으로 Key - value 쌍을 저장하고 가져올 수 있다. (O(1))

하지만, 아래와 같이 Key에 해당하는 값이 커질 수 록 낭비하는 공간이 많다. (메모리 낭비가 심하다)

이 문제를 보완하기 위해 해시 테이블이 등장하게 된다.

해시 함수

하나의 Key와 그 Key에 해당하는  value를 합쳐서 Key-value 쌍이라 부르며

이때 하나의 key는 하나의 value만 가지고 있어야 한다.

(파이썬에서는 Hash함수를 제공한다.)

특정 값을 원하는 범위의 자연수로 바꿔주는 함수 (여기서 특정 값 = Key)

키의 범위 아무리 커도 원하는 범위의 자연수로 바꿀 수 있게 된다.

---

해시 함수의 조건

1. 한 해시 테이블의 해시 함수는 결정론적이어야 한다.

=> 같은 Key를 넣었을때 항상 같은 결과가 나와야 한다.

2. 결과 해시값이 치우치지 않고 고르게 변환되어야 한다.

3. 빠르게 계산 할 수 있는 함수여야 한다. (O(1))

=> 해시 테이블은 모든 연산을 할때 해시함수를 거치게 되므로 해시함수가 느리다면?? 이하 생략.

위 3가지를 만족하는 함수라면 해시 함수로 이용할 수 있다.

---

해시 함수의 예시

간단하게 나누기와 곱셈 기타 방법으로 해시 함수를 구현 할 수 있다.

나누기

def hash_function_remainder(key, array_size):
    """해시 테이블의 key를 나누기 방법으로 0 ~ array_size - 1 범위의 자연수로 바꿔주는 함수"""
    return key % array_size

---

곱셈

이해를 돕기 위해 예시로 key가 200이고 사용하려는 배열 크기가 30이라고 할게요.

1. 먼저 0 < a < 10<a<1 인 아무 값 a를 정합니다. 일단 임의로 0.6666로 정할게요
2. 그다음에 이 a에 key를 곱합니다. 그러니까 0.666에 200을 곱하면 133.32이 되는데 이때 정수 부분은 버리고 소수 부분만 남깁니다. 0.32가 남습니다.
3. 마지막으로 남은 소수 부분에 배열의 크기를 곱해줍니다. 0.32 * 30 하면 9.6이 되죠. 이번엔 소수점 부분을 버리고 9만 남깁니다.

단계가 조금 많아서 헷갈릴 수도 있는데요. 왜 이 방법이 원하는 범위의 자연수를 리턴하는지 생각해볼까요? a와 key를 곱한 값의 정수 부분을 버리면 그 결과 값은 0.xxxx 이런 식으로 0과 1 사이의 소수가 나올 수밖에 없겠죠? 0과 1 사이의 소수에 테이블의 크기를 곱해버리면, 다시 0과 테이블 크기 사이의 수가 나오죠. 그러니까 0.0001에 테이블 크기 30을 곱하면 0.003이 나오고 0.9999에 테이블 크기 30을 곱하면 29.997이 나오는데요. 항상 0보다 크거나 같고 테이블 크기인 30보다는 작은 숫자가 나옵니다. 그리고 여기서 소수점 뒷자리를 버리니까 원하는 범위의 자연수를 구할 수 있습니다.

def hash_function_multiplication(key, array_size, a):
    """해시 테이블의 key를 곱셈 방법으로 0 ~ array_size - 1 범위의 자연수로 바꿔주는 함수"""
    temp = a * key # a와 key를 곱한다
    temp = temp - int(temp) # a와 key를 곱한 값의 소숫점 오른쪽 부분만 저장한다
    
    return int(array_size * temp) # temp와 배열 크기를 곱한 수의 자연수 부분만 리턴한다
        

 

해시 테이블

이전과 같이 (배열, 링크드리스트)순서 데이터를 저장하는 것이 아닌

key-value 데이터를 효율적으로 저장하고 관리할 수 있도록 하는 자료구조이다.

간단하게 말해서 배열과 해시 함수를 함께 사용하는 자료구조다.

1. 원하는 크기의 배열을 만든다.

2. 해시 함수를 이용해 Key를 원하는 범위의 자연수로 바꾸고 이 자연수를 배열의 인덱스로 사용한다.

3. 해시 함수 결과 값 인덱스에 Key - value 데이터를 저장한다.

---

충돌

해시 테이블에 데이터를 저장할때 

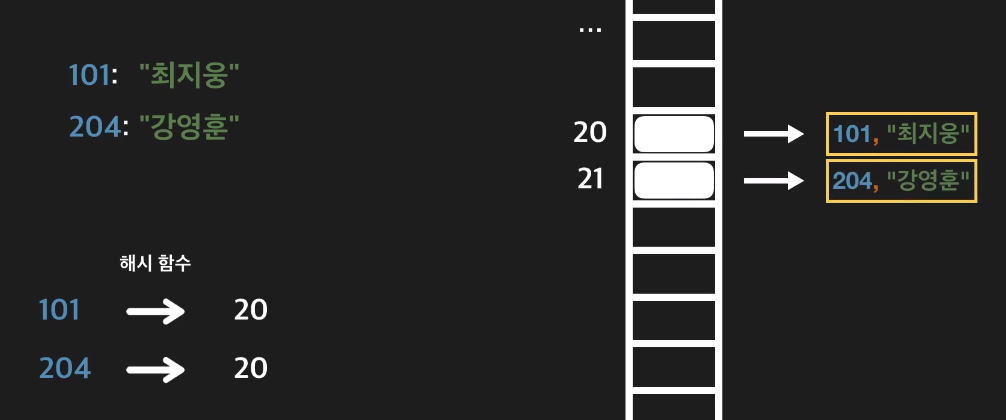
101, 204의 Key가 같은 해시 값을 반환한다고 생각해보자.

이 경우 아래와 같이

하나의 인덱스의 2개의 데이터 쌍을 저장해야하는 경우가 발생한다.

공간에 2개의 value가 저장되므로 key-value가 1:1로 매핑되어야 하는 해시 테이블의 특성에 위배된다.

이처럼 이미 사용하고 있는 인덱스에 새로운 데이터를 저장해야하는 경우 충돌이 일어났다고 표현한다.

 

 

---

충돌 해결 방안 1. Chaining(체이닝)

충돌이 일어나면 데이터를 엮겠다는 의미이다.

여기서 데이터를 연결시켜주는 자료구조인 링크드리스트를 이용해 체이닝을 한다!

간단하게 말하자면 

배열의 인덱스에 새로운 링크드 리스트를 만들고 Key-value 데이터를 Node로 만들고 저장한다.

 

이때, Node는 아래와 같이 Key, value 속성을 가져야한다.

 

링크드 리스트에서와 같이 다음 노드에 대한 레퍼런스를 이용해 엮어놓으면 원하는 Key- value 데이터를 모두 저장할 수 있다.

---

충돌 해결 방안 2. Open Addressing (개방주소법)

충돌이 일어났을때 다른 비어있는 인덱스를 찾아 저장하는 방법이다.

같은 20의 해시값이 나왔지만 20이 이미 채워져있어 21인덱스를 찾아 저장한 모습이다.

 

이때 비어있는 인덱스를 찾는 방법은 여러가지가 있다고 한다.

그 중 2가지만 살펴보자

1. 선형 탐사(Liner Probing) => 가장 기본적인 방법

2. 제곱 탐사(Quadratic probing)

 

선형 탐사 (Liner Probing)

충돌이 일어났을 때, 비어있는 인덱스를 하나씩 순서대로 선형적으로 찾는 방법.

 

제곱 탐사 (Quadratic probing)

충돌이 일어났을 때, 비어있는 인덱스를 제곱을 한 값들을 이용해 찾는 방법이다.

인덱스 10의 값을 저장하자고자 할때

선형의 경우 11 , 12 로 찾으며

제곱의 경우 11 (1의 제곱 뒤) , 15 (2의 제곱 뒤 -> 11 + 2^2), 21 (3의 제곱 뒤 -> 15 + 2^3)..

초기 해시값이 같으면 동일한 폭으로 탐색하기 때문에 효율성이 떨어진다.

 

시간 복잡도

1. Chaining(체이닝)을 사용하는 해시 테이블

먼저 1번의 경우 최악의 경우가 발생하는 상황은

저장하는 모든 key-value 데이터가 하나의 링크드 리스트에 저장되는 경우이다.

데이터의 수를 n 이라 하면, 최악의 경우 링크드 리스트의 길이도 n이다.

이때 탐색, 저장, 삽입, 삭제 등의 연산들은 모두 Key를 이용해 저장된 링크드 리스트 노드를 탐색하는 과정을 포함하기 때문에 모두 최악의 경우 O(n)이다.

 

하지만!

모두 같은 링크드 리스트에 저장되는 경우는 거의 발생하지 않는다. 

분활 상황 분석을 이용해 합리적으로 구해보자면 아래와 같다.

 

링크드 리스트 전체 길이 n 이 아닌, 링크드 리스트의 평균 길이에 비례한다고 말할 수 있다.

평균 점수를 구할때를 생각해보면 모든 합의 점수를 학생 수로 나눠 평균을 구하지 않는가?

마찬가지로 각 인덱스에 저장된 링크드 리스트들의 평균 길이를 생각하는 것이다.

해시 테이블에 총 들어가 있는 key-value 데이터의 수 : n

해시 테이블이 사용하는 배열의 크기를 : m 이라 한다면

링크드 리스트 평균 길이는 n/m이 되고 시간복잡도는 O(n/m)으로 표현 하는 것도 문제가 없다.

여기서 가정해야할 사항으로 해시 테이블을 만들 때 항상 충분히 여유롭게 총 저장하는 key-value 데이터의 수와 

해시 테이블이 사용하는 배열의 크기를 비슷하거나 작다고 가정은 해야한다.

항상 어느 정도까지는 n = m 이라는 약속이라고 한다. 이 약속만 지켜주면 아래와 같이 표현 할 수 있다!

실제로 해시 테이블을 사용할때는 대부분 O(1)이 걸린다느 가정하에 사용한다고 한다.

하지만 알고리즘에서는 예외인 상황도 중요하므로

해시 테이블의 탐색, 삽입, 삭제 연산들은 최악의 경우 O(n)이 걸리지만, 평균적으로 O(1)이라 말한다!

---

2. Open Addressing (개방주소법)을 사용하는 해시 테이블

체이닝과 마찬가지로 탐색, 저장, 삽입, 삭제 등의 연산들은 모두 Key를 이용해 저장된 링크드 리스트 노드를 탐색하는 과정을 포함하기 때문에 모두 최악의 경우 O(n)이다.

 

여기서 load factor를 추가로 설명해보자

load factor란

해시 테이블이 얼마나 차있는지를 나타내는 변수이다.

해시 테이블에 총 들어가 있는 key-value 데이터의 수 : n

해시 테이블이 사용하는 배열의 크기를 : m 

 

Open Addressing 해시 테이블의 연산들을 분석할때 load factor가 굉장히 중요한 역할을 한다.

(그만큼 해시 테이블이 얼마만큼 차 있는지가 중요하게 작용한다)

해시 테이블 안에 배열의 크기보다 많은 데이터를 저장할 수 없기 때문에 알파는 항상 1보다 작다고 가정한다.

 

결과적으로 Open Addressing 해시 테이블에서 평균적으로 탐사를 해야하는 횟수는 아래 기대값을 갖는다.

만약 배열이 100칸, 데이터의 수가 90개 일경우 알파는 0.9가 되며

기대값은 10이 나오게 된다. 즉 빈 인덱스를 찾기 위해 평균 10개보다 적은 인덱스를 확인해도 된다는 뜻이기도 하다. 알파가 0.5만 되어도 (해시 테이블이 반정도 차있다면) 기대값은 2보다도 작다.

위에서 같이 

실제로 Open Addressing 해시 테이블을 사용할때도 대부분 O(1)이 걸린다느 가정하에 사용한다고 한다.

해시 테이블의 탐색, 삽입, 삭제 연산들은 최악의 경우 O(n)이 걸리지만, 평균적으로 O(1)이라 말한다!

---

추가로, 파이썬에서의 딕셔너리 자료형은 해시 테이블로 구현되어있다고 알고 있었다.

결론만 말하자면 이 두가지는 다른 개념이다.

=> 추상 자료형(딕셔너리) 와 자료구조(해시 테이블)는 의미 자체가 다르다.

이는 추상 자료형 딕셔너리에서 더 파보도록 하자.

---

자료구조 기본기를 익히고 싶다면 굉장히 좋은 출발점이 될 강의로 생각한다.

출처 : 코드잇(자료구조)

자료 구조 | 코드잇 (codeit.kr)