TIL.65 알고리즘과 선형_이진 탐색

먼저 알고리즘이란 무엇일까

Algorithm

: 알고리즘(라틴어, 독일어: Algorithmus, 영어: algorithm 알고리듬[*], IPA: [ǽlɡərìðm])은 수학과 컴퓨터 과학, 언어학 또는 관련 분야에서 어떠한 문제를 해결하기 위해 정해진 일련의 절차나 방법을 공식화한 형태로 표현한 것, 계산을 실행하기 위한 단계적 절차를 의미한다.

알고리즘은 연산, 데이터 마이닝(기계 학습) 또는 자동화된 추론을 수행한다. 산법(算法), 셈법, 계산 절차 등으로 번역되기도 한다.

(출처 : wikipedia ko.wikipedia.org/wiki/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98)

알고리즘 - 위키백과, 우리 모두의 백과사전

 

간단하게 말해, 알고리즘이란 "문제를 해결 하는 절차" 이다.

세상의 다양한 문제에 대해 어떻게 접근하고 어떻게 해결 할 것인가를 수학, 논리적으로 해결을 해나가는 "방법" 이라 할 수 있다.

알고리즘의 해답을 사람마다 생각, 접근방식 등의 차이가 있으며 이렇게 풀어낸 알고리즘은 분석을 통해 좋고 나쁨을 평가 할 수 있다.

이러한 알고리즘은 "개발 전체"에 사용되며, 더 나아가 "문제 해결 전체"에 해당된다 말할 수 있다.

개발자에게 있어 알고리즘은 피할 수 없는 숙명이다.

 

알고리즘을 평가하는 기준은 크게 2가지가 있다.

1. 시간 분석(Time_analysis) : 작성 알고리즘으로 얼마나 빠른 시간 안에 문제를 해결 할 수 있는가

2. 공간 분석(Space_analysis) : 작성 알고리즘이 얼마나 적은 용량(메모리)를 효율적으로 사용하는가

이 2가지 기준을 무조건 지키는 경우만있는 경우는 아니다.

용량을 포기하고 속도를 높히거나, 속도를 포기하고 용량을 줄이는 알고리즘이 굉장히 많다고 한다.

 

탐색 / 선형탐색 , 이진탐색

오늘은 이와 관련하여 알고리즘의 가장 첫단추라 할 수 있는 탐색

그 중, 가장 기초가 되는 선형/이진 탐색에 대해 알아보자

1. 선형 탐색 : 말그대로 순차적으로 차례차례 탐색하는 것을 말한다.

이는 정렬되지 않은 데이터들을 순차적으로 접근해 원하는 데이터를 찾는 경우이다.

만약 정렬이 되어 있다면 이진탐색으로 원하는 데이터를 찾는게 훨씬 빠르다.

 

2. 이진 탐색 : 데이터가 정렬도어 있는 배열에서 원하는 데이터를 찾아내는 방법을 말한다

Divide and Conquer{"분할정복의 한 방식" : "분할 분할 분할 하여 원하고자하는 값을 찾는 과정"}

이는 500페이지가 넘는 전공서적에서 내가 원하는 페이지를 찾고자 할때

반으로 나누어 반에 해당 하는 값과 비교하며 앞에 있을지 뒤에있을지 판단하는 방법과 같다.

 (대/소 비교를 통해 데이터 탐색을 진행한다)

정렬되어 있지 않는 데이터는 이진탐색을 이용할 수 없다.

---

아래 배열을 이용해 선형탐색과 이진탐색을 비교해보자

 

선형탐색으로 숫자 1을 찾을 경우 단 1번 만으로 원하는 값을 찾을 수 있으나

숫자 700을 찾고자하는 경우 10번 탐색을 하여 원하는 값을 찾을 수 있다.

숫자가 10개 수열에서 선형탐색은 평균적으로 약 5.5회 탐색횟수를 가지게 된다.

 

실제로 아래와 같이 10개의 숫자 중 임의적으로 하나의 숫자를 골라 몇번만에 찾는지 알아보자

선형탐색을 이용

탐색횟수를 1만번 반복하여 평균을 알아보자.

실제로 5.5에 근접한 탐색횟수를 확인하였다.

import random

numList = (1,5, 7, 13, 50, 120, 300, 320, 400, 700)

for k in range(10):
	cntSum = 0
    for i in range(10000):
    rundNum = numList[random.randint(0, 9]]
    for n in numList:
    	cntSum += 1
        if n == rndNum:
        	break
	print(cunSum/10000)

---

이진탐색을 이용

이진탐색

시작, 끝 그리고 Key가 존재한다.

첫 인덱스 : 시작

끝 인덱스 : 끝

키 : 시작+끝 // 2 ==> 둘의 평균인 4.5에서의 정수부분이 키의 위치가 된다

---

어떤 V 라는 값을 찾는다 가정해보자

V 가 Key 와 일치한다면 -> 바로 종료

만약 V가 Key  와 일치하지 않는다면 -> V는 Key 반드시 작거나 클것이다.

---

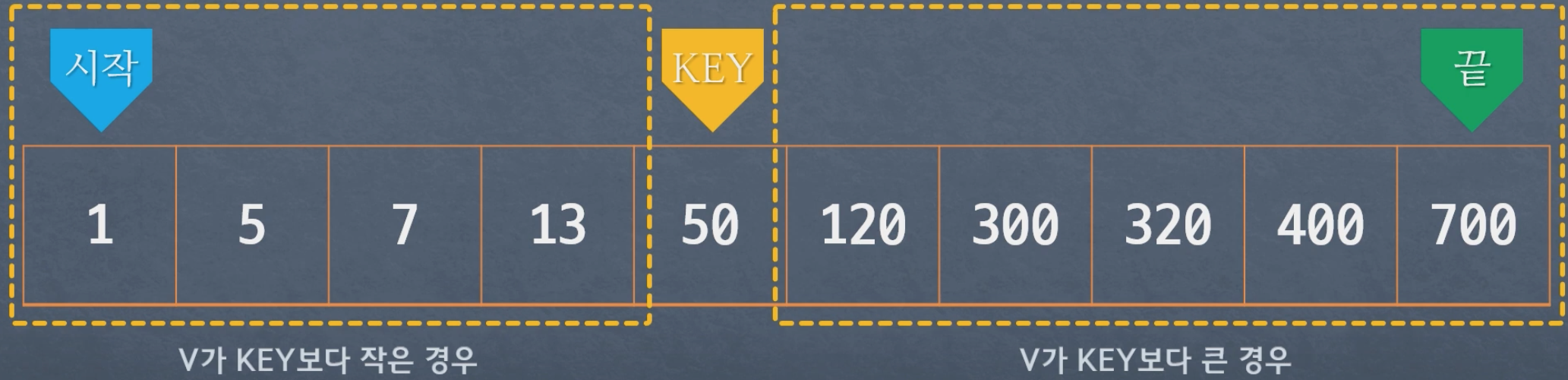
여기서 우리는 V가 Key보다 크다고 가정해보자

V는 Key의 다음 위치부터 끝까지의 범위 중에 존재한다고 판단 할 수 있다

key 의 다음위치를 시작위치로 변경하고 변경된 시작위치와 변경되지 않은 끝 위치를 기준으로 다시 Key의 위치를 지정한다

V가 Key 값과 일치한다면 종료

만약 V가 Key값과 일치하지 않는다면 역시나 V는 작거나 클것이다.

---

이번에는 작다고 가정해보자

V는 Key의 이전 위치와 시작까지의 범위 중에서 존재한다고 판단할 수 있다.

 

key 의 이전위치를 끝위치로 변경하고 변경되지 않은 시작위치와 변경된 끝 위치를 기준으로 다시 Key의 위치를 지정한다

 

이런식으로 계속 진행하다보면 결국 시작위치와 끝위치가 겹치게 되는데 (시작 위치와 끝 위치가 겹침)

해당 수열에 찾고자하는 값이 반드시 존재한다면 여기(시작, 끝 위치가 겹치는 시점)까지만 진행하면 된다.

V가 120이었다면 키와 비교하고 종료

만약 V가 300이었다면 시작과 끝 위치가 같아지고 이는 시작 바로 뒤가 끝이며, 원하느 값은 끝 위치에 있느 값이란걸

알 수 있다.

 

만약 찾고자하는 값이 없는 경우가 있다면, 

시작과 끝 위치가 겹친상태에서 한번 더 진행을 한다

그렇게되면 시작 위치가 끝 위치보다 커지게 되는데 이 상태를 값이 없다고 판단하는 기준으로 삼게된다.

---

이진탐색을 이용해 처음부터 V = 300이라는 값을 찾고싶었다면 총 4번의 탐색만으로 찾을 수 있었다.

만약, 선형탐색을 이용했다면 7번 탐색하여 찾을 수 있을 것이다.

 

이진탐색도 위와 마찬가지로 

탐색횟수를 1만번 반복하여 평균을 알아보자.

실제로 3에 근접한 탐색횟수를 확인하였다.

import random

numLsit = (1, 5, 7, 13, 50, 120, 300, 320, 400, 700)

for k in range(10):
	cutSum = 0
    for i in range(10000):
    	start = 0
        end = len(numList) -1
        key = int((start+end)/2)
        V = random.randint(start, end)
        while True:
        	cntSum += 1
            if numList[Key] == numLsit[V] or start == end:
            	break
            elif numList[key] < numList[V]:
            	start = key + 1
            	key = int((start+end)/2)
            else:
            	end = key -1
                key = int(start+end)/2)
	print(cntSum/10000)

---

5.5와 3의 크기가 크지않게 느껴질 수 있다.

하지만, 요소의 수가 많아진다면 어떨까? 많아지면 많이질수록 이 둘의 차이는 점점 커질게 될 것이다.

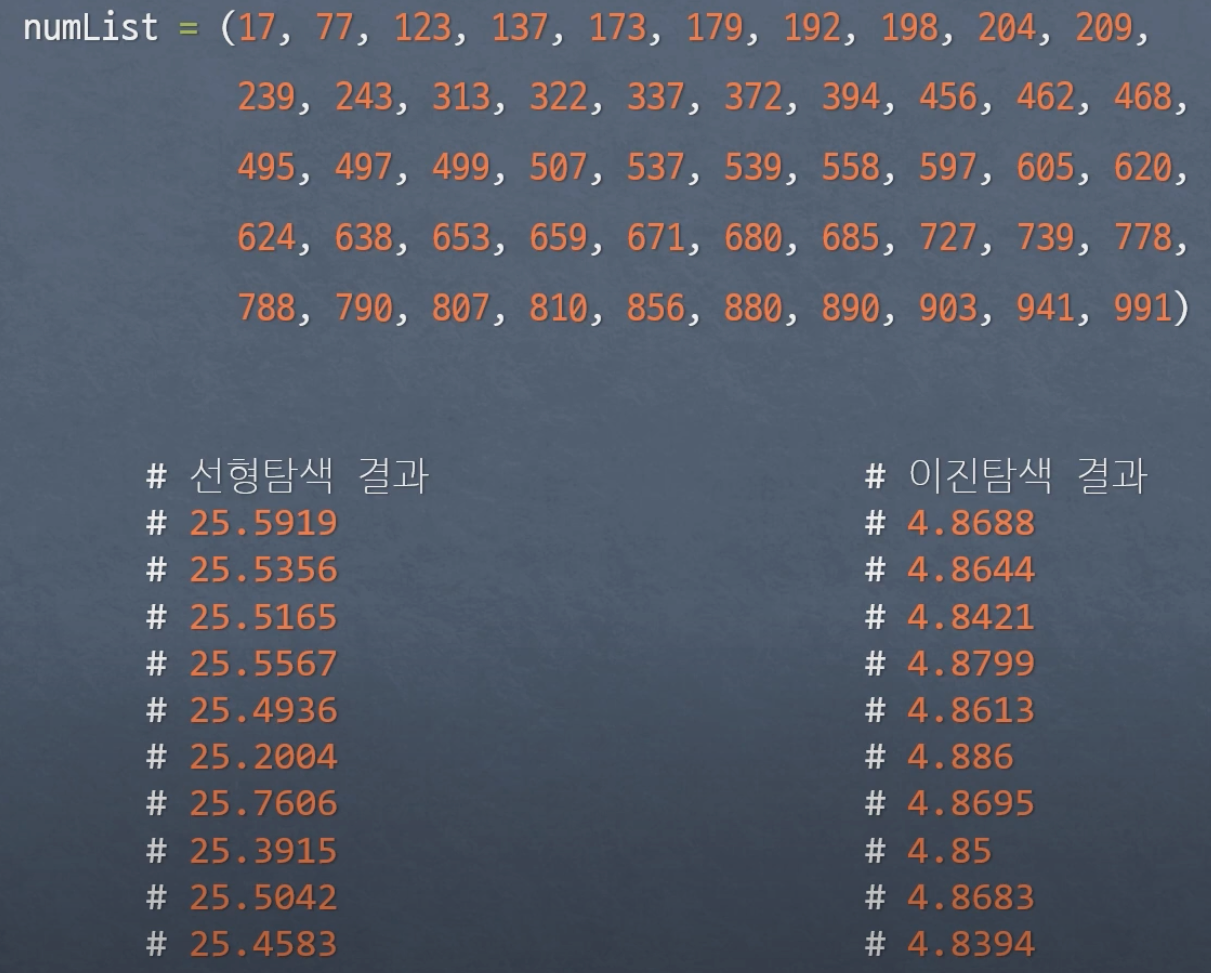
수열의 길이가 길어질 수록 그 차이는 눈에 띄게 커질 것이며 이는 시간복잡도 개념과 연관되어

아래와 같은 배열에서 찾고자할때는 당연히 이진탐색이 효율적이라는 것을 알 수 있다.

 

 

결론

선형 탐색의 장점

구현이 쉽고, 직관적이다

선형 탐색의 단점

느리다.

이진탐색의 장점

속도가 빠르다

이진탐색의 단점

자료구조 안의 내용들이 정렬이 되어있을 경우에만 사용할 수 있다.

---

코드로 구현한 것만봐도 이진탐색의 코드가 훨씬 길고 복잡하다고 느낄수있다.

하지만 개발자는 효율적인 알고리즘을 구현하기 위해 끉임없이 생각하고 생각하며

보다 더 효율적인 알고리즘을 고안해내는 능력이 필요하다

 

우리는 끉임없이 효율적인 알고리즘을 찾고자 생각하고 또 생각하고 이렇게 생각할 수 있는 관점을 가지는게 중요하다고 생각한다

실제 알고리즘 문제를 풀다보면 이 사람이 선형탐색과 이진탐색 알고리즘의 매커니즘을 제대로 이해하고 있는지 아닌지가

초보 개발자인 내 눈에도 보이기 때문에 항상 이를 고민하고 이러한 고민을 즐기는 개발자가 되자

 

출처 : 파이썬클래스 Youtube

www.youtube.com/watch?v=rBRu9T8v37w