빅오 표기법 (O, big-O)

빅오란 입력값이 무한대로 향할때 함수의 상한을 설명하는 수학적 표기 방법이다.

빅오는 점근적 실행 시간을 표기할때 가장 널리 쓰이는 수학적 표기 방법이다. 여기서 점근적 실행 시간이란 간단하게 n이라는 입력값이 무한대로 커질떄의 실행 시간의 추이를 의미한다. 따라서 충분히 큰 입력값에서의 알고리즘의 효율성에 따라 수행 시간이 크게 차이가 날 수 있다.

점근적 실행 시간을 달리 말하면 "시간 복잡도"라 할 수 있다. 

시간 복잡도의 사전적 정의

어떤 알고리즘을 수행하는 데 걸리는 시간을 설명하는 계산 복잡도를 의미하며, 계산 복잡도를 표기하는 대표적인 방법이 빅오 표기법인 것이다.

빅오로 시간 복잡도를 표현할때는 최고차항만 표기힌다.

4n^2 + 3n +4
==>

O(n^2)

최고 차항만 표기 한다 -> O(n^2) 만 표기하나는 뜻이다.

리미트 n이 무한대로 커질 경우를 생각해보자 먼저 상수항 4는 의미가 없으므로 제외하며, 3n 의 경우도 입력값이 무한대로 커질경우 4n^2 이 1000000000000000이 된다고 했을때 차지 하는 비중은 크게 의미가 없으므로 동일하게 제외시킨다.

결국 위 식에서의 빅오 표기법의 주체는 최고차항인 n^2만을 표기한다.

 

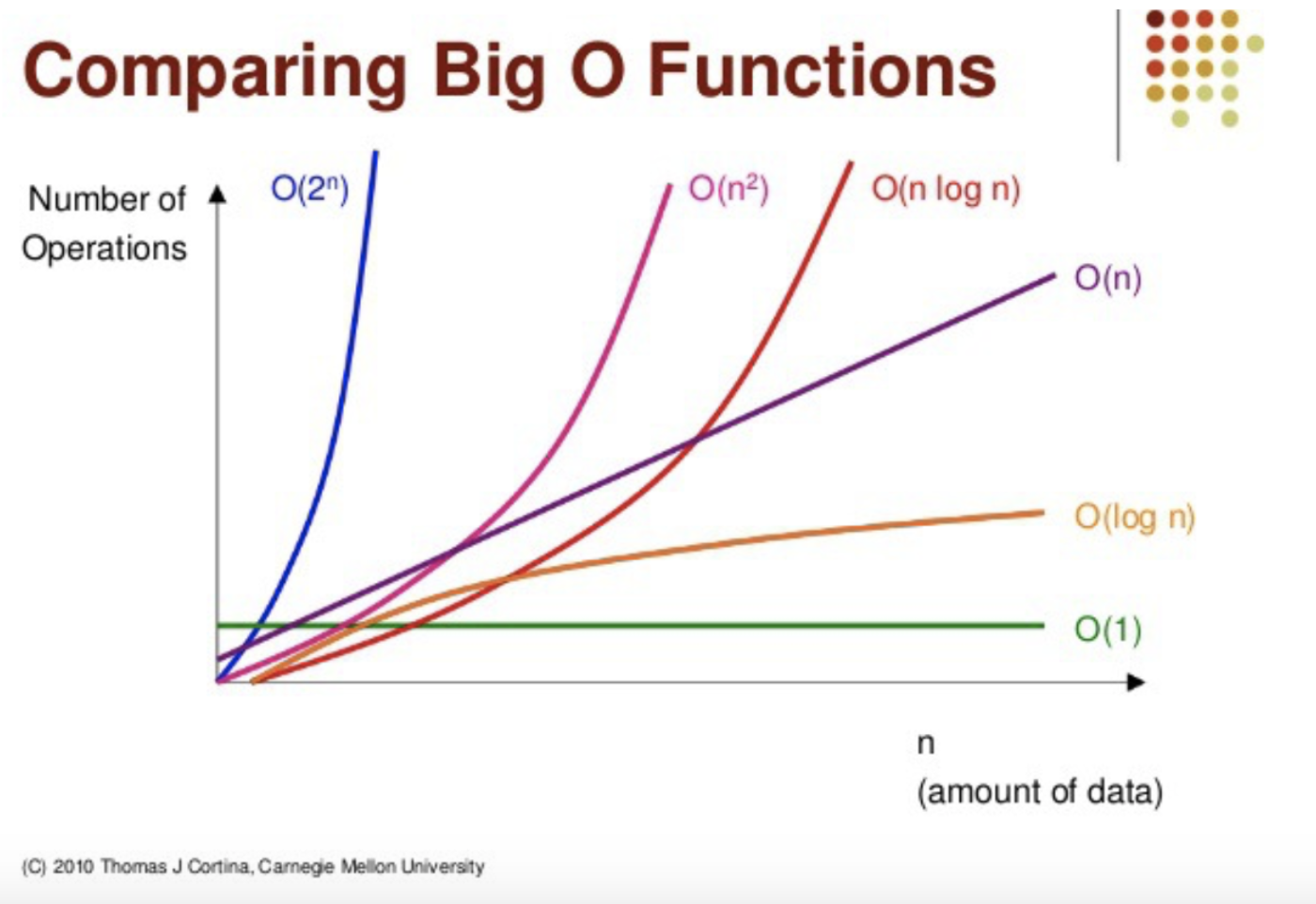
빅오 표기법의 종류

O(1) : 입력값에 상관없이 일정한 실행시간을 최고!의 알고리즘이라 할 수 있다. 하지만 상수 시간에 실행된다 해도 상수값이 상상 이상으로 클 경우 사실상 일정한 시간의 의미가 없다. 최고의 알고리즘이 될 수 있지만 그만큼 신중해야 한다.

O(log n) : 로그는 매우 큰 입력값에서도 크게 영향을 받지 않는 편이다. 매우 견고한 알고리즘으로 이진 탐색의 경우가 이에 해당한다.

O(n) : 알고리즘을 수행하는데 걸리는 시간은 입력값에 비례한다. 이러한 알고리즘을 선형 시간 알고리즘이라 부른다. 정렬되지 않은리스트에서 최대 또는 최솟값을 찾는 경우가 해당되며 모든 입렵값을 적어도 한 번 이상은 살펴봐야 한다.

O (n log n) : 병합 정렬등의 대부분 효율이 좋은 알고리즘이 이에 해당 한다. 아무리 좋은 알고리즘이라 할지라도 n log n 보다 빠를 수 없다. 입력값이 최선일 경우, 비교를 건너 뛰어 O(n)이 될 수 있다.

O(n^2)  : 버블 정렬 같은 비효율저긴 정렬 알고리즘이 이에 해당 한다.

O(2^n) : 피보나치의 수를 재귀로 계산하는 알고리즘이 이에 해당 한다. n^2와 혼동되는 경우가 있는데 2^n이 훨씬 더 크다.

O(n!) : 가장 느린 알고리즘으로 입력값이 조금만 커져도 계산이 어렵다.

https://medium.com/@callmedevmomo/%EC%9B%B9-%EA%B0%9C%EB%B0%9C%EC%9E%90%EB%A5%BC-%EC%9C%84%ED%95%9C-%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0%EC%99%80-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-01-%EB%B9%85%EC%98%A4-%ED%91%9C%EA%B8%B0%EB%B2%95-ff369f0efc1d

 

빅오 표기법은 시간 복잡도 외에도 공간 복잡도를 표현하는데 널리 쓰인다. 

알고리즘은  "시간과 공간이 트레이드오프 관계이다" (트레이드 오프 : 하나가 증가하면 다른 하나는 감소한다.)

즉, 빠른 알고리즘은 공간을 많이 사용하고, 공간을 적게 차지하는 알고리즘은 실행 시간이 느리다는 것이다. 물론, 아닌 알고리즘도 드물게 존재하지만 대부분 의 경우 트레이드오프 관계가 성립되며 이는 알고리즘의 주요한 특징 중 하나이다.

 

상한 & 최악

위의 빅오 표기법을 설명하며 상한, 최선, 최악이란 단어를 사용했다. 그렇다면 이 것들은 무슨 말일까?

빅오(O)는 상한을 의미한다. 하한을 의미하는 빅오메가, 평균을 의미하는 빅세타가 있지만 보통 빅오만을 사용한다.

여기서 중요한 포인트는 상한 = 최악의 경우 와 혼동하는 것이다.

빅오 표기법은 정확하게 쓰기에는 너무 길고 복잡한 함수를 "적당히 정확하게" 표현하는 방법일 뿐,

최악의 경우/ 평균적인 경우의 시간 복잡도와는 아무런 관계가 없는 개념이다.

 

빅오 표기는 복잡하 함수 f(n)이 있을 경우 이 함수의 실행 상한과 하한을 의미힌다.

즉, 가장 빨리 실행될때가 하한, 가장 늦게 실행될때가 상한을 뜻한다.

이 중 가장 늦게 실행될 때를 빅오(O), 가장 빨리 실행될 때를 빅오메가(Ω), 평균을 빅세타(θ) 로 지칭한다.

n이 작을때, 즉 n0 이하 일때의 값이 작은 경우는 무시하며! 빅오 표기법은 n이 매우 클 때의 전체적인 큰 그림에 집중한다.

 

결론, 빅오 표기법은 주어진(최선/평균/최악) 경우의 수행 시간의 상한을 나타낸다