힙_1

힙

완전 이진 트리를 기 이진 트리를 기본으로 하는 자료구조로 트리의 일종이며 아래 두개의 조건을 만족하는 트리이다.

최댓값 , 최솟값을 쉽게 추출 할 수 있는 자료구조이다.

이러한 힙은 힙_2에서 설명할 우선순위 큐를 위하여 만들어진 자료구조라 한다.

 

1. 형태 속성 : 힙은 완전 이진 트리여야 한다.

2. 힙 속성 : 모든 노드의 데이터는 자식 노드들의 데이터보다 크거나 작아야 한다.

- Heap은 부모 노드가 항상 자식 노드보다 크거나 같아야 하는 경우(max heap)와 부모 노드가 항상 자식 노드보다 작거나 같아야 하는 경우(min heap)로 나눌 수 있다.

최댓값을 추출하고자 할때는 부모 노드가 자식 노드보다 항상 큰 max heap으로

최솟값을 추출하고자 할때는 부모 노드가 자식 노드보다 항상 작은 min heap을 활용하면 된다. (root 노드를 추출하기 쉬운 환경을 구성해준다)

---

10은 8, 6 보다 크고

8은 7, 4 보다 크고

6은 2 보다 크다. => 형태 속성 + 힙 속성 모두 만족하므로 힙이라 할 수 있다.

---

힙 속성을 만족하지 않음

---

힙 구현해보기(heapify)

완전 이진 트리는 동적 배열로 구현할 수 있으며

파이썬의 리스트 자료구조를 사용하여 구현해보자.

트리에서 알아보았듯 부모 노드 인덱스를 통해 왼쪽/오른쪽 자식의 인덱스를 알아 낼 수 있다.

현재 아래의 트리는 형태 속성만 만족하고 있는 상태이다.(완전 이진 트리)

Tree = [None, 15, 5, 12, 14, 9, 10, 6, 2, 11 , 1]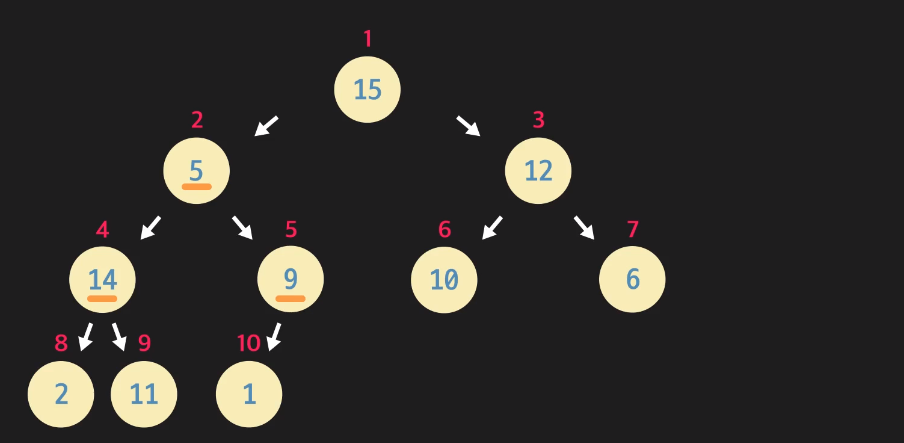

---

1. 부모노드 5와 자식 노드 14, 9 총 3가지를 비교하여 큰 값을 부모 노드로 만들어 준다.

2. 왼쪽 자식 노드가 더 크기 때문에 14를 부모노드로 서로의 자리를 바꿔준다.

---

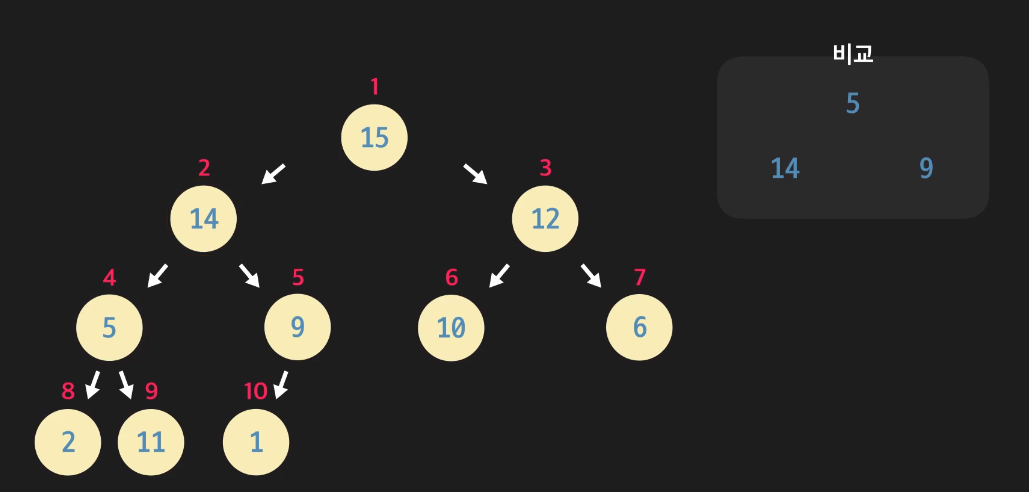
3. 위 1, 2번 과정을 반복한다. 

Tree = [None, 15, 14, 12, 11, 9, 10, 6, 2, 5 , 1]

결과적으로 해당 트리는 힙 속성을 만족하게 되고 힙이라 부를 수 있게 된다.

위 과정 처럼 해당 노드가 맞는 위치를 찾을 때까지 재배치해주는 알고리즘을 heapify 라 부른다.

---

heapify 시간 복잡도

Tree = [None, 15, 5, 12, 14, 9, 10, 6, 2, 11 , 1]
heapify
Tree = [None, 15, 14, 12, 11, 9, 10, 6, 2, 5 , 1]

최악의 경우는 파라미터로 맨 위의 루트 노드가 맨 밑의 leaf 노드까지 내려가는 경우이다.

이러한 최악의 경우는 총 트리의 높이 만큼 비교하고 재배치 시킨다.

트리의 노드의 개수가 N 이라 할때

힙은 완전 이진 트리로 높이 lg(N)이므로 heapify의 시간복잡도는 O(logN)이라 할 수 있다.

heapify만 보았을때는 O(logN) 이라 할 수 있지만

결국 우린 heapify를 트리를 힙으로 만들기 위해 사용하므로 

힙 트리를 만드는데 최악의 경우 heapify를 N번 반복해야하 하므로

힙 트리를 만드는데 걸리는 시간복잡도는 O(N x logN) => O(NlogN)이다.

 

출처 : 코드 잇(자료구조)

자료 구조 | 코드잇 (codeit.kr)