이진 탐색 트리_1

이진 탐색 트리

트리의 일종으로 이진 트리이면서 이진 탐색 트리의 속성을 만족하는 트리를 이진 탐색 트리라고 부른다.

영어로는 Binary Search Tree 라고 부른다.

이진 탐색 트리를 사용하면 저장한 데이터를 쉽게 찾아 올 수 있다.

 

이진 트리는 각 노드가 최대 2개의 자식 노드만 가질 수 있는 트리를 말한다.

이진 트리에서는 모든 노드가 2개, 1개, 0개의 자식 노드만 가지고 있다.

여기서 이진 탐색 트리의 속성은 아래와 같다.

1. 특정 노드를 기준으로, 특정 노드의 왼쪽 부분 트리에 있는 모든 노드는 특정 노드의 데이터보다 작아야 한다.

2. 특정 노드를 기준으로, 특정 노드의 오른쪽 부분 트리에 있는 모든 노드는 특정 노드의 데이터보다 커야 한다.

루트 노드가 아닌 모든 루트에 적용되는 속성이다.

아래는 각각 특정 노드가 루트 노드(8) 일때와 특정 노드(3) 일때 모두 이진 탐색 트리 속성을 만족한다.

---

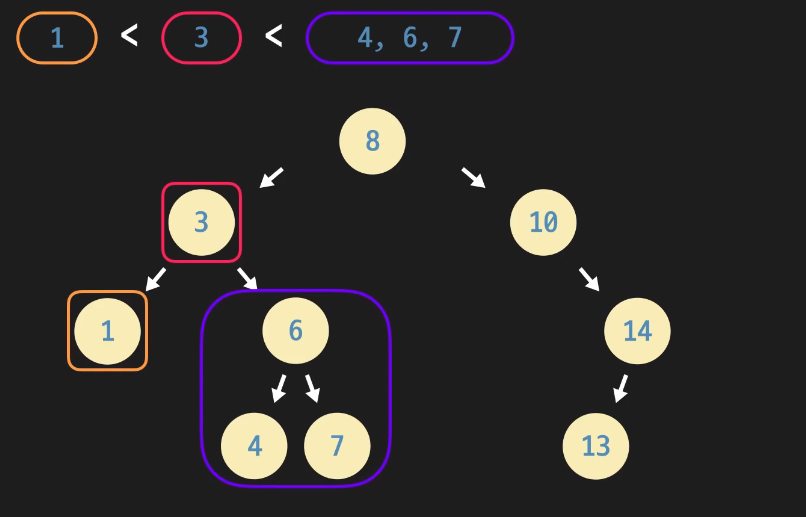
이진 탐색 트리 구현하기

이진 탐색 트리는 이진 트리이긴 하나, 힙과 달리 완전 이진 트리라는 보장은 없다.

따라서, 배열 또는 파이썬 리스트를 이용해 구현하지 않고 노드 클래스와 인스턴스를 생성하여 연결시키는 방법으로 구현하며 노드가 왼쪽/오른쪽 자식 노드에 대한 레퍼런스에 추가로 부모에 대한 레퍼런스를 갖는 방식으로 구현한다.      (링크드 리스트를 구현하는 방법과 유사하다.)

 

이진 탐색 트리의 핵심은 

노드를 어떻게 연결하고

노드를 어떻게 삭제하고

노드를 어떻게 찾는지가 핵심이다. 

---

삽입

이진 탐색 트리에 데어터를 삽입할때는 이진 탐색 트리의 속성을 유지해야 한다.

아래 데이터 13을 삽입하는 예시를 보자.

 

이진 탐색 트리에서는 삽입하고 재배치를 하는것이 아니라 먼저 삽입이 되어야 할 데이터의 위치를 먼저 파악한다.

그 후 루트 노드인 12를 시작으로 대소 비교를 해가며 13이 자리하게 될 위치를 찾는다.

13을 삽입할때는 12, 18, 15 순으로 비교하며 15의 왼쪽 노드에 위치해야함을 찾을 수 있다.

삽입 방법을 아래와 같이 정리할 수 있다.

1. 새로운 노드를 생성한다.

2. 루트 노드부터 비교하면서 새로운 노드가 저장될 위치를 찾는다.

3. 찾은 위치에 새롭게 만든 노드를 연결해준다.

 

탐색

특정 데이터를 갖는 노드를 리턴하는 연산으로 보통 탐색 연산을 먼저 정리하였는데 삽입 연산으로 탐색을 어떻게 했는지 잠깐 알아보긴 하였다. 삽입에서 데이터가 들어갈 위치를 찾는 연산과 비슷하다.

아래 이진 탐색 트리에서 데이터 12를 탐색하는 예시를 보자.

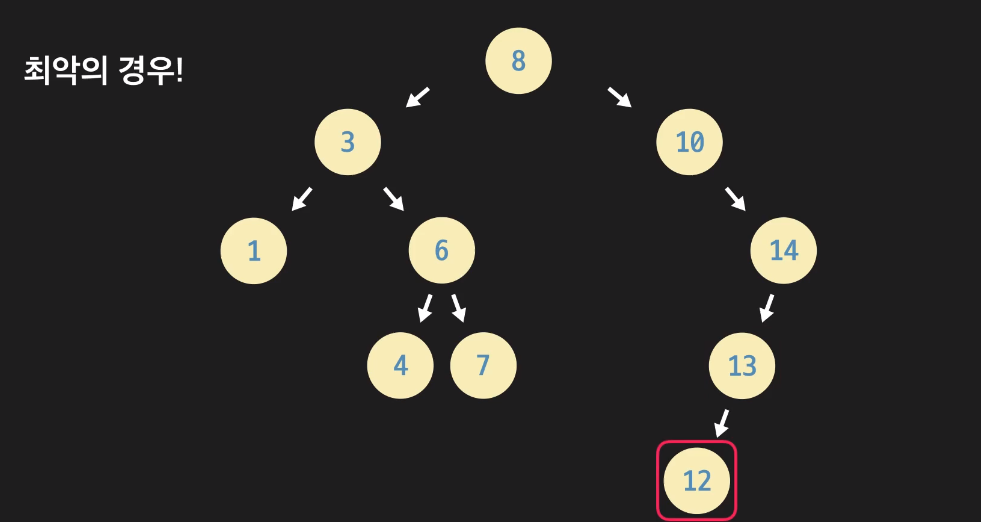
이진 탐색 트리의 속성을 이용하여 루트 노드로 부터 주어진 노드의 데이터를 비교하는 방법으로 내려간다.

탐색 방법을 아래와 같이 정리할 수 있다.

1. 주어진 노드의 데이터와 탐색하려는 데이터를 루트 노드에서 부터 시작하여 비교한다.

2. 루트 노드와 비교하며 주어진 노드가 더 크다면 오른쪽 자식으로, 작다면 왼쪽 자식으로 이동하며 비교한다.

3. 주어진 노드와 일치하는 노드를 찾으면 리턴한다.

---

삭제

이진 탐색 트리에서 데이터를 삭제하는 연산은 고려해야 하는 경우의 수가 많다.

삭제 연산에서는 위의 탐색 연산을 사용하여 지우고자 하는 데이터(노드)를 먼저 찾아야 한다.

삭제 방법을 아래와 같이 정리 할 수 있다.

1. 삭제하고자 하는 데이터의 SUCCESSOR 노드를 찾는다.

2. 삭제하고자 하는 데이터(노드)의 데이터 속성에 SUCCESSOR 데이터를 저장한다.

3. SUCCESSOR 노드를 삭제한다. (연결을 끊고 맺음으로써 삭제한다.)

삭제하는 경우 아래와 같은 3가지의 경우의 수를 다 고려해줘야 한다.

    경우 1 : 삭제하려는 데이터가 leaf 노드인 경우

    경우 2 : 삭제하려는 데이터가 하나의 자식 노드만을 가지고 있는 노드일 경우

    경우 3 : 삭제하려는 데이터가 두 개의 자식 노드를 모두 가지고 있는 경우 

---

경우 1

삭제하려는 데이터가 leaf 노드인 경우

리프 노드인 경우 자식 노드가 하나도 없는 상태로

이는, 왼쪽/오른쪽 자식 노드에 대한 레퍼런스가 모두 None인 상태를 말한다.

또한 삭제하고자 하는 노드가 리프 노드를 만족함과 동시에 부모 노드의 왼쪽/오른쪽 자식일 경우를 고려한다.

이진 탐색 트리는 각 노드들의 인스턴스를 연결하는 방식으로 연결을 끊고 다시 맺어줌으로써 삭제하고자 하는 노드를 트리에서 제외시킨다.

class BinarySearchTree:
    """이진 탐색 트리 클래스"""
    def __init__(self):
        self.root = None


    def delete(self, data):
        """이진 탐색 트리 삭제 메소드"""
        node_to_delete = self.search(data)  # 삭제할 노드를 가지고 온다
        parent_node = node_to_delete.parent  # 삭제할 노드의 부모 노드

        # 지우려는 노드가 리프 노드인 경우
        if node_to_delete.left_child is None and node_to_delete.right_child is None:
            # 지우려는 노드가 리프노드이면서 동시에 부모 노드 일 경우
            if node_to_delete is self.root:
                self.root = None
            # 지우려는 노드가 부모 노드의 왼쪽 자식 노드인 경우
            if parent_node.left_child is node_to_delete:
                parent_node.left_child = None
            # 지우려는 노드가 부모 노드의 오른쪽 자식 노드인 경우    
            else:
                parent_node.right_child = None

---

경우 2

삭제하려는 데이터가 하나의 자식 노드만을 가지고 있는 노드일 경우

경우 2에서도 왼쪽 자식노드만을 가지고 있는지 오른쪽 자식 노드만을 가지고 있는지에 따라 경우의 수를 고려해줘야한다.

class BinarySearchTree:
    """이진 탐색 트리 클래스"""
    def __init__(self):
        self.root = None


    def delete(self, data):
        """이진 탐색 트리 삭제 메소드"""
        node_to_delete = self.search(data)  # 삭제할 노드를 가지고 온다
        parent_node = node_to_delete.parent  # 삭제할 노드의 부모 노드

        # 경우 1: 지우려는 노드가 leaf 노드일 때
        if node_to_delete.left_child is None and node_to_delete.right_child is None:
            if self.root is node_to_delete:
                self.root = None
            else:  # 일반적인 경우
                if node_to_delete is parent_node.left_child: 
                    parent_node.left_child = None
                else:
                    parent_node.right_child = None

        # 경우 2 : 지우려는 노드가 하나의 자식만 있는 노드인 경경우
        # 2- 1 : 지우려는 노드가 왼쪽 자식 노드만 가지고 있는 경우
        elif node_to_delete.left_child is not None and node_to_delete.right_child is None:
            # 지우려는 노드가 왼쪽 자식만 가진 루트 노드일 경우
            if node_to_delete is self.root:
                self.root = node_to_delete.left_child
                self.root.parent = None
            # 지우려는 노드가 부모 노드에 왼쪽에 위치하는 경우
            elif node_to_delete.data < parent_node.data:
                parent_node.left_child = node_to_delete.left_child
                node_to_delete.left_child.parent = parent_node
            # 지우려는 노드가 부모 노드에 오른쪽에 위치하는 경우
            else:
                parent_node.right_child = node_to_delete.left_child
                node_to_delete.left_child.parent = parent_node
                
        # 2-2 : 지우려는 노드가 오른쪽 자식 노드만 가지고 있는 경우
        else:
            # 지우려는 노드가 오른쪽 자시만 가진 루트 노드일 경우
            if node_to_delete is self.root:
                self.root = node_to_delete.right_child
                self.root.parent = None
            # 지우려는 노드가 부모 노드에 왼쪽에 위치하는 경우
            elif node_to_delete.data > parent_node.data:
                parent_node.left_child = node_to_delete.right_child
                node_to_delete.right_child.parent = parent_node
            # 지우려는 노드가 부모 노드에 오른쪽에 위치하는 경우
            else:
                parent_node.right_child = node_to_delete.right_child
                node_to_delete.right_child.parent = parent_node

---

경우 3

삭제하려는 데이터가 두 개의 자식 노드를 모두 가지고 있는 경우 ( 예시 12)

삭제하고자 하는 노드의 오른쪽 자식 노드를 find_min 함수의 파라미터로 전달한다.

(find_min은 부분 이진 탐색트리에서 가장 작은 노드를 리턴하는 정적 메서드이다.

삭제하고자 하는 노드 12의 오른쪽 부분 트리에 있는 모든 수는 12보다 큰 수이다. 따라서 find_min 함수로 리턴된 노드는

12 보다 큰 노드들 중 가장 작은 노드를 반환하는데 이를 이진 탐색 트리에서는 SUCCESSOR 라 부른다.

위의 예시에서 successor는 14가 되고 successor는 12보다 항상 크며, SUCCESSOR는 왼쪽 자식 노드를 가질 수 없다.

(왼쪽 자식 노드를 갖는 순간 모순이 된다. 만약 successor가 13의 왼쪽 자식 노드를 가지고 있다고 치면 반환되는 successor는 14가 아닌 13을 반환할 것이다. 결국 successor는 왼쪽 자식 노드를 가질 수 없다.)

반횐된 successor(노드) 를 이용, 삭제하고자하는 노드의 data를 successor의data로 저장해주고 경우에 따라 연결을 재정의해주면 된다.

solution_1 과 solution_2 중 solution_2의 경우가 주석을 따라 읽다보면 더 이해가 빠를 것 같다.

    def delete(self, data):
        """이진 탐색 트리 삭제 메소드"""
        node_to_delete = self.search(data)  # 삭제할 노드를 가지고 온다
        parent_node = node_to_delete.parent  # 삭제할 노드의 부모 노드

        # 경우 3: 지우려는 노드가 2개의 자식이 있을 때
        # 지우려는 노드의 오른쪽 자식 노드를 이용해 successor 노드를 찾는다.
        else:
            successor_node = self.find_min(node_to_delete.right_child)
            node_to_delete.data = successor_node.data
            
            """ solution_1 """
            # 3-1 : successor 노드가 삭제하려는 노드의 오른쪽 부분 트리에서  특정 부모 노드 아래 위치하는 경우
            if successor_node is successor_node.parent.left_child:
                # if else문을 사용할 필요없이 successor 노드가 오른쪽 자식 노드가 없다면 알아서 None으로 지정된다.
                # successor 노드가 오른쪽 자식 노드를 갖는경우와 갖지 않는 경우를 한 줄로 표현한 것이다.
                successor_node.parent.left_child = successor_node.right_child
            # 3-2 : successor 노드가 삭제하려는 노드의 바로 밑 오른쪽 자식인 경경우
            else:
                # 위와 마찬가지로 successor 노드가 오른쪽 자식 노드를 갖는 경우와 갖지 않는 경우를 한 줄로 표현한 것이다. 
                successor_node.parent.right_child = successor_node.right_child
            
            # 추가 조건
            # successor가 오른쪽 자식 노드를 갖는 경우 만을 따로 취급하여 부모 노드를 새롭게 지정해준다.
            if successor_node.right_child is not None:
                successor_node.right_child.parent = successor_node.parent
            
            """ solution_2 """
            # 3-1 : successor 노드가 삭제하려는 노드의 바로 밑 오른쪽 자식인 경우
            if successor_node is node_to_delete.right_child:
                if successor_node.right_child is not None:
                    node_to_delete.right_child = successor_node.right_child
                    successor_node.right_child.parent = node_to_delete
                successor_node.parent = None
            # 3-2 : successor 노드가 삭제하려는 노드의 오른쪽 부분 트리에서  특정 부모 노드 아래 위치하는 경우
            else:
                if successor_node.right_child is not None:
                    successor_node.right_child.parent = successor_node.parent
                    successor_node.parent.left_child = successor_node.right_child
                successor_node.parent.left_child = None
                successor_node.parent = None
                    
    @staticmethod
    def find_min(node):
        """(부분)이진 탐색 트리의 가장 작은 노드 리턴"""
        # 코드를 쓰세요
        temp = node  # 탐색 변수. 파라미터 node로 초기화

        # temp가 node를 뿌리로 갖는 부분 트리에서 가장 작은 노드일 때까지 왼쪽 자식 노드로 간다
        while temp.left_child is not None:
            temp = temp.left_child      

        return temp  

---

시간 복잡도

삽입

1. 새로운 노드를 생성한다.

O(1)

2. 루트 노드부터 비교하면서 새로운 노드가 저장될 위치를 찾는다.

비교하는 과정은 트리의 높이 만큼 노드 데이터를 비교하면서 내려와야 한다.

아래의 예시처럼 최악의 경우 트리의 높이를 H 라 한다면

루트 노드 부터 비교 해야 하며, 트리의 높이는 0에서 시작하므로 16이 삽입될 자리는 찾는데  12, 18, 15, 17 총 4번의 비교를 해야하고 이는 H + 1과 같다

이때 시간 복잡도는 O(H)

3. 찾은 위치에 새롭게 만든 노드를 연결해준다.

O(1)

따라서 총 시간 복잡도는 O(H) 이다.

이때 요소의 갯수가 아닌 트리의 높이라는 점을 기억하자.

---

탐색

탐색 연산의 시간 복잡도는 삽입에서의 데이터를 찾는 과정과 비슷하다.

결국 데이터를 서로 비교하며 트리를 내려와야 하는데

최악의 경우는 트리의 가장 깊이 있는 노드의 데이터를 탐색할때이다.

아래 예시에서 데이터 12를 탐색하는 경우 8, 10, 14, 13, 12 총 5번을 비교해야하며 이는 트리의 높이 H+1과 같다.

(루트 노드 부터 비교 해야 하며, 트리의 높이는 0에서 시작)

따라서, 총 시간 복잡도는 O(H)이다.

---

삭제

삭제 연산의 시간복잡도는 공통적으로 삭제하고자 하는 노드를 탐색하는 과정이 선행된다. O(H)

탐색 이후는 아래와 같은 경우에 따른 시간 복잡도를 알아보자.

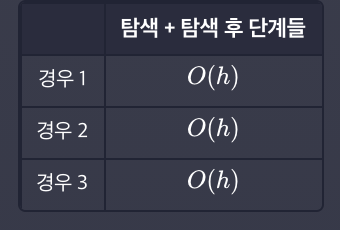
경우 1 : 삭제하고자 하는 데이터가 리프 노드 일 경우

탐색한 노드로부터 레퍼런스만을 변경하므로 노드의 갯수나 트리의 높이에 영향을 받지 않는다. 

O(1)

경우 2 : 삭제하고자 하는 데이터가 하나의 자식 노드를 가지고 있을 경우

탐색한 노드로부터 어떤 노드가 주어지든 위 경우와 같이 래퍼런스 2개의 연결만을 수정한다.

O(1)

경우 3 : 삭제하고자 하는 데이터가 두 개의 자식 노드를 가지고 있을 경우

삭제하고자 할때는 successor 노드를 찾는 과정(find_min) 은 트리의 높이에 비례하므로 O(H)

successor 노드의 데이터를 저장하는 과정은 O(1)이라 생각할 수 있으나, 이진 탐색 트리에서 데이터를 저장하는 과정은 결국 저장해야할 노드까지 접근하는 시간 O(H)이 필요하기 때문에 O(H)라고 한다!

successor가 오른쪽 자식 노드가 있으면 O(2), 없으면 O(1)이 걸리기 때문에 결국 O(1)

따라서 총 시간 복잡도는 O(H + H + 1) => O(H)이다.

출처 : 코드 잇(자료구조)

자료 구조 | 코드잇 (codeit.kr)