그래프_1

그래프

그래프는 연결 관계에 있는 데이터를 저장하는 자료구조이다.

그래프는 노드라는 가장 작은 단위의 데이터로 이루어져 있는데, 각 노드들의 관계가 동등한 위치에 있을 경우 그래프를 적용하여도 무방할 것 같다.

자료구조를 공부해야 하는 이유는 상황에 맞는 방식으로 데이터를 저장하고 사용하기 위해서이다.

데이터 사이에 어떤 관계가 있는지 파악하고 그에 맞는 적절한 자료구조를 사용하기 위함이다.

앞, 뒤와 같은 순서 데이터를 저장하기 위해서는 배열, 링크드 리스트 같은 선형 자료구조를

상, 하 관계와 같은 계층 데이터를 저장하기 위해서는 트리와 같은 계층 자료구조를 사용하면 된다.

---

그렇다면 그래프는 언제 사용하는 걸까?

그래프는 연결 관계에 있는 데이터를 저장한다고 하였는데 이는 실제로 우리 생활에서 무궁무진한 예시들이 존재한다.

위치, 경로, 친구 관계, 인스타그램의 팔로우 관계 등 모두 그래프를 사용하여 데이터를 관리할 수 있다.

내비게이션 앱의 목적지간의 최단 거리, 소요 시간 및 메신저 앱의 친구 관계, 배달앱의 실시간 배송 위치 등 모두 이 그래프 자료구조를 사용하여 데이터를 관리하고 있다. 여태껏 공부하였던 자료구조 중 가장 흥미롭고 인트로부터 재미있는 녀석이라는 생각이 든다.

---

그래프의 기본 개념

친구 관계의 예시를 통해 그래프의 기본 개념들을 알아보자.

노드

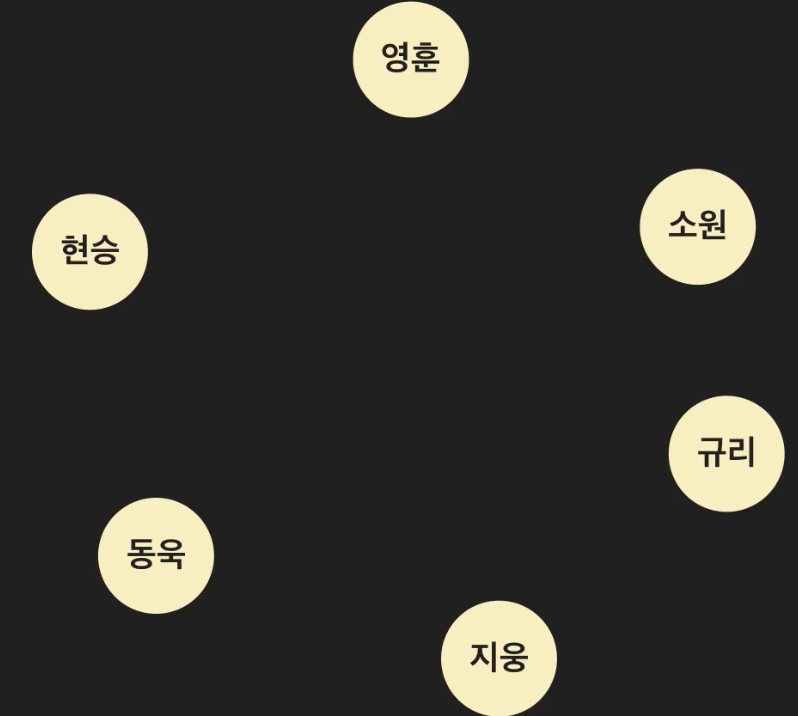
그래프에서는 기본 데이터 단위로 노드를 사용한다.

친구 관계에서는 하나의 그래프 노드를 한명의 사람이라 표시하면 된다.

 

---

에지(Edge)

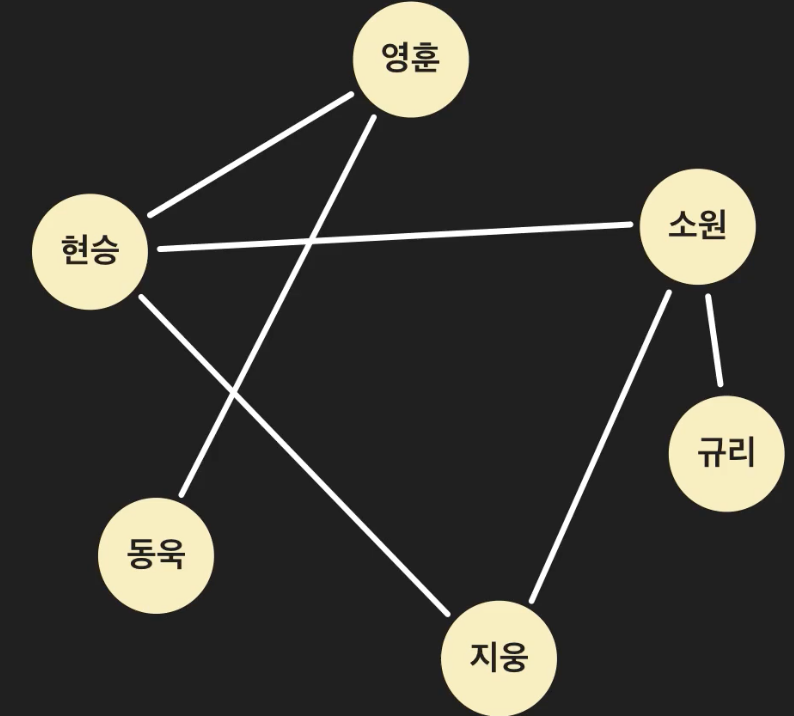
노드 사이의 관계를 에지(에지)라 부른다.

영훈과 현승 사이에 에지를 만들어 서로 친구 관계에 있음을 나타낼 수 있다.

영훈과 현승 사이를 잇는 에지는 현승, 영훈 에지 or 영훈, 현승 에지라고 부른다.

에지로 각 노드를 연결하여 친구 관계를 나타낼 수 있다.

---

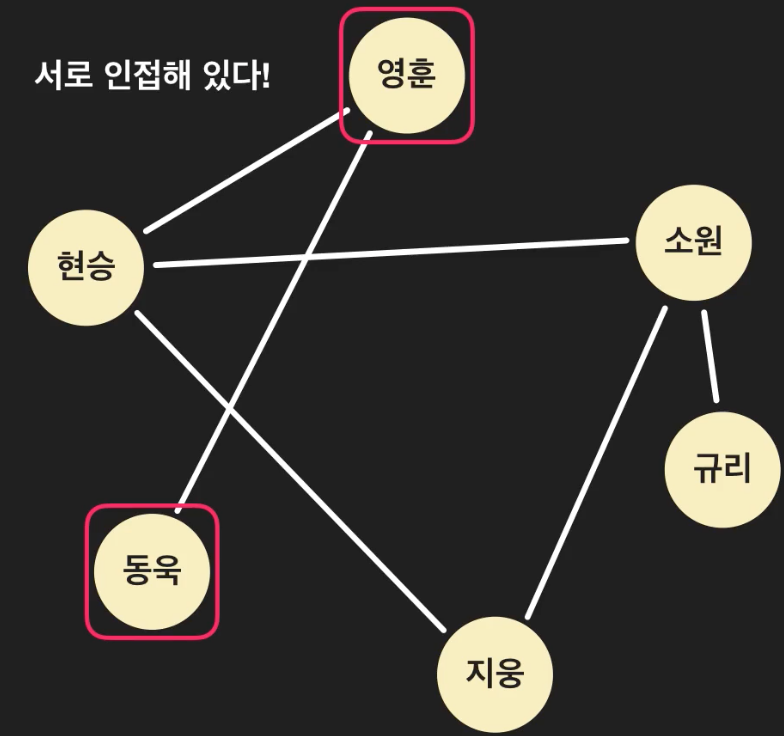
인접

두 노드가 에지로 연결되어 있을 때 서로 인접해 있다고 표현한다.

영훈과 동욱은 서로 인접해 있다.

반면, 지웅과 규리는 서로 인접해 있지 않다고 표현한다.

---

경로

지웅과 규리는 서로 인접해있지는 않지만, 둘 다 소원과 친구 관계에 있다.

따라서, 소원을 통해 연결되어 있으며

이때 지웅과 규리를 잇는 이 길을 경로라고 부르며

지웅과 규리는 지웅 - 소원- 규리 or 규리 - 소원 - 지웅 경로를 통해 연결되어 있다고 표현한다.

경로 안에 있는 에지의 수를 거리라고 부르며 이때 경로의 거리는 2라고 표현한다.

두 노드 사이에 가장 거리가 작은 경로를 최단 경로라 부르며, 2보다 작은 경로는 없으므로 최단 경로는 2가 된다.

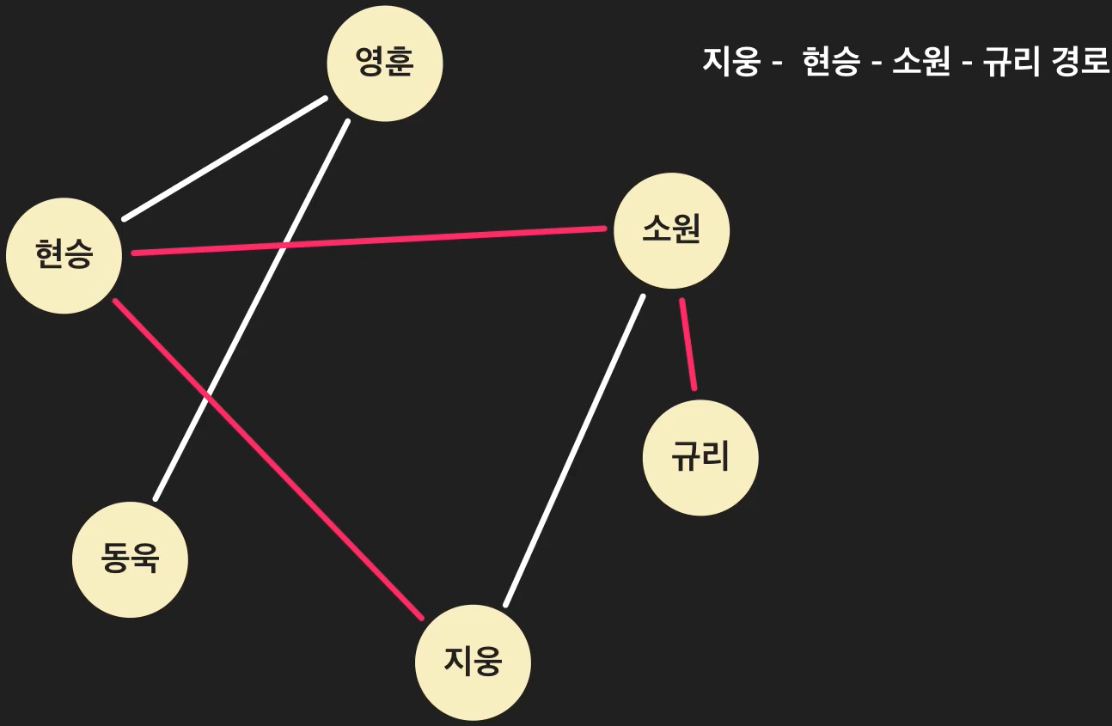
지웅과 규리 사이에는 경로가 하나 더 존재하는데, 실제로 각 노드 사이에는 무수히 많은 경로가 존재하거나 아예 없을 수 있다.

지웅과 규리는 지웅-현승-소원-규리 경로로 연결되어있으며, 이때의 경로의 거리는 4이다.

---

사이클

특정 노드에서 다시 해당 노드로 돌아오는 경로를 사이클이라 부른다.

지웅 - 현승 - 소원- 지웅과 같은 경로를 사이클이라 부른다.

---

차수

한 노드가 가지고 있는 에지의 개수를 차수라고 부른다.

영훈은 에지를 2개 가지고 있으므로 영훈의 차수는 2이다.

이때 차수는 큰 의미를 갖는데, 친구 관계에서의 차수는 각 노드의 친구의 수를 나타내는 지표로 사용할 수 있다.

소원이 몇 명의 친구를 가지고 있는지 알기 위해서는 소원의 차수를 알아보면 되는 것이다.

---

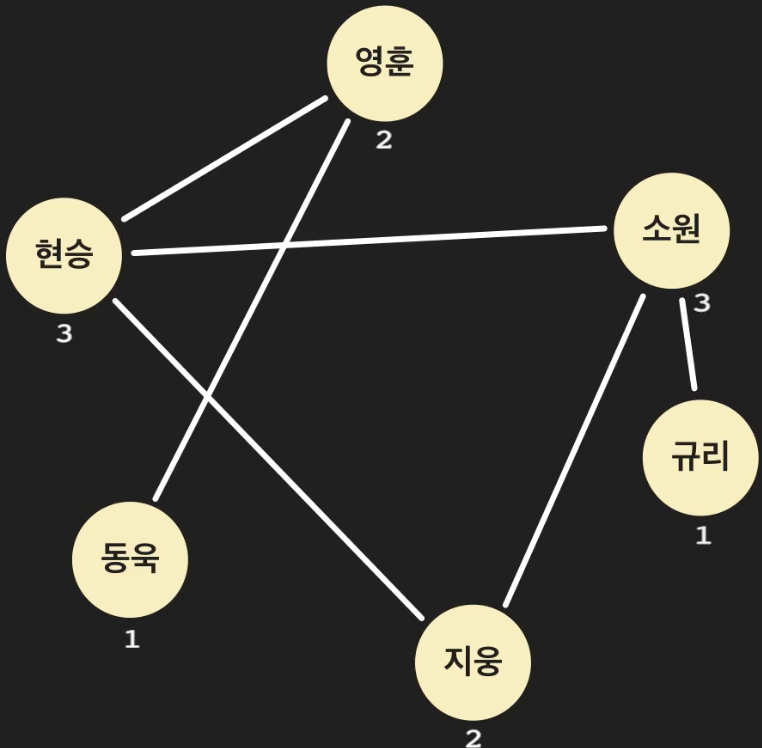
그래프의 종류

위 예제처럼 에지가 쌍방향인 경우

즉, A가 B와 친구라면 B도 A와 친구 관계가 성립하는 관계이다.

하지만 인스타그램의 팔로우와 같이 A가 B를 팔로우한다고 해서 B는 A를 팔로우하지 않는 관계를 정의하기 위해선 위의 그래프로는 연결 관계를 정의할 수 없을 것이다.

그래프는 크게 방향성과 가중치에 따라 분류가 가능하다.

1. 에지의 방향성에 따라

1-1. 무방향 그래프 (undirected graph)

ex ) 친구 관계와 같이 에지의 방향성이 없는 관계를 표현할 때 사용

1-2. 방향 그래프 (directed graph)

ex ) 인스타그램의 팔로우와 같이 엣지의 방향성이 있는 관계를 표현할 때 사용

2. 가중치에 따라

2-1. 무가 중치 그래프

2-2. 가중치 그래프

에지에 특정 숫자 값을 지정하여 관계를 표현할 때 사용 

아래와 같이 각 노드 간 거리, 위치 데이터를 사용하고 싶은데 모드 같은 길이의 에지로 표현하기에는 무리가 있기에 에지에 숫자 값을 지정하여 나타내는 그래프이다.

---

방향 그래프

인스타그램 팔로우를 예시로 아래와 같은 방향 그래프를 나타낼 수 있다.

방향을 쌍방향으로도 표시할 수 있으며, 서로를 맞팔하고 있는 경우도 나타 낼 수 있다.

---

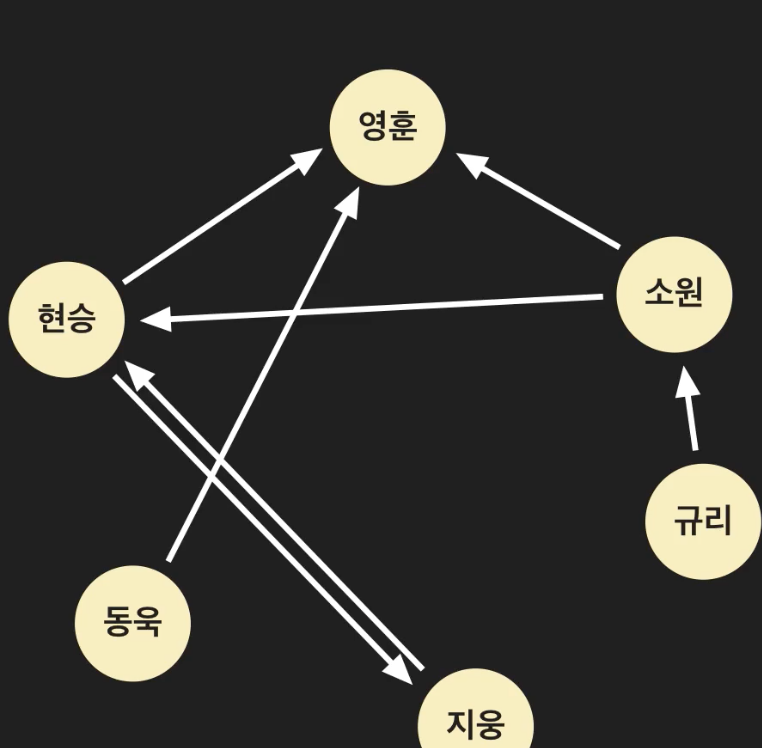
방향 그래프에서의 에지

방향 그래프에서는 에지가 떠나는 노드를 항상 앞에 쓰고, 에지가 들어가는 노드를 뒤에 적어준다.

즉, 현승 - 지웅 에지라고 부를 수 있지만, 지웅- 현승 에지라고는 부를 수 없다.

---

방향 그래프에서의 경로

에지들의 방향 때문에 영훈에서 지웅까지 가는 경로가 없다!

---

방향 그래프에서의 차수

노드에서의 나가는 에지의 수 = 출력 차수

노드로 들어오는 에지의 수 = 입력 차수로 라고 표현한다.

현승의 차수의 경우 출력 차수는 2이고, 입력 차수는 1이다.

---

가중치 그래프에서의 거리

가중치가 없는 무가 중치 그래프에서의 거리는 에지의 개수였지만

가중치 그래프에서의 거리는 모든 에지의 가중치의 합이다.

인천-LA-뉴욕의 경로가 거리는 2가 아니라 14이다.

---

 

그래프의 연결성

그래프는 모든 노드끼리 연결되어 있을 필요는 없다.

세상 모든 사람들이 친구 관계가 아니듯 아래와 같이 보기에는 나누어져 있는 그래프로 보일지 모르지만 실제로는 하나의 SNS 유저 그래프이며 극단적으로 아예 에지가 없이 노드로만 구성된 그래프도 존재할 수 있다!!

---

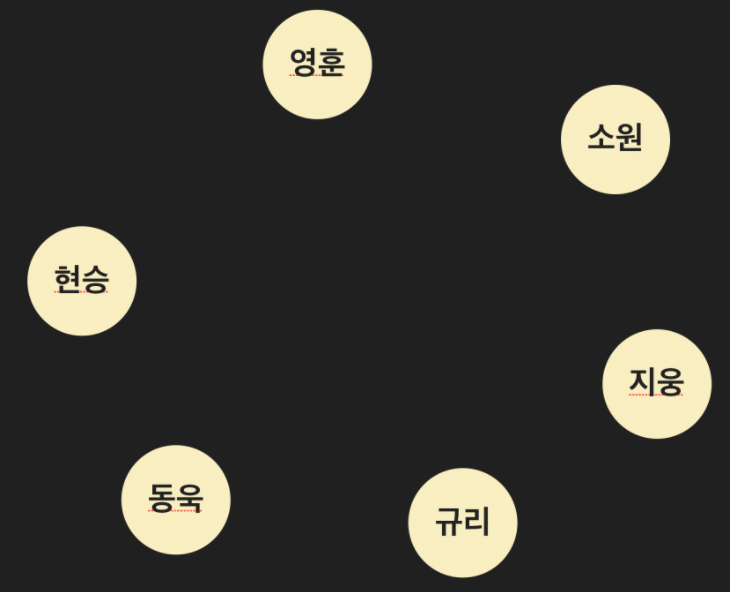
SUMMARY

노드 : 그래프에서의 기본 단위

엣지 : 두 노드의 직접적인 연결 데이터 및 관계

- 방향 그래프에서의 에지 : 방향성을 갖는다.

- 가중치 그래프에서의 에지 : 연결관계 + 추가 정보(거리, 친밀도 등등)

차수 : 하나의 노드에 연결된 에지의 개수

- 무방향 그래프에서의 차수 : 하나의 노드에 연결된 에지의 개수

- 방향 그래프에서의 차수 : 출력 차수와 입력 차수로 나뉨

경로 : 한 노드에서 특정 노드까지 가는 길

경로의 거리

   - 비 가중치 그래프 : 한 경로에 있는 에지의 수

   - 가중치 그래프 : 한 경로에 있는 엣지의 가중치의 합

최단 경로 : 두 노드 사이의 경로 중 거리가 가장 짧은 경로

사이클 : 한 노드에서 시작해서 같은 노드로 돌아오는 경로

 

출처 : 코드 잇(자료구조)

자료 구조 | 코드 잇 (codeit.kr)