그래프 탐색_BFS, DFS

그래프 탐색

보통 탐색은 주어진 조건에 맞는 데이터를 찾는 것을 의미 하지만

그래프에서의 탐색은 하나의 노드를 시작점으로 연결된 노드들을 모두 찾는 것을 탐색이라고 말한다.

자료구조 안에 저장된 모든 데이터를 도는 것을 순회라고 하는데 

따라서, 그래프에서의 탐색도 하나의 노드에서 연결된 모든 노드를 돌기 때문에 그래프 순회라고도 부르기도 한다.

(그래프 탐색과 그래프 순회는 같은 말이다.)

 

 

그래프를 탐색하며 알 수 있는 정보

그래프를 탐색하면 그래프의 구조에 대해 의미 있는 정보들을 알아낼 수 있다.

1. 주어진 두 노드가 경로를 통해 연결되어있는지 여부

2. 주어진 두 노드 사이의 최단 경로를 알아낼 수 있다.

대표적으로 두가지 정도가 있으나 정렬 등 많은 문제에서 그래프 탐색을 사용하여 문제를 해결할 수 있다고 한다.

---

그래프 탐색 알고리즘

그래프 탐색 알고리즘은 각 노드들을 어떤 순서로 탐색하는지에 따라 크게 아래와 같이 2종류로 나뉜다.

1. Breadth First Search (BFS)

너비 / 우선/ 탐색 

특정 노드를 시작으로 인접한 노드를 먼저 찾는 탐색 방법

2. Depth First Search (DFS)

깊이/ 우선/ 탐색

특정 노드를 시작으로 다음 분기(branch)를 넘어가기 전 해당 분기를 완벽하게 탐색하는 방법

---

BFS

그래프에서 너비를 우선적으로 탐색한다는 말은 무엇일까?

아래 예시로 알아보자.

탐색을 마친 노드는 회색으로 표시한다.

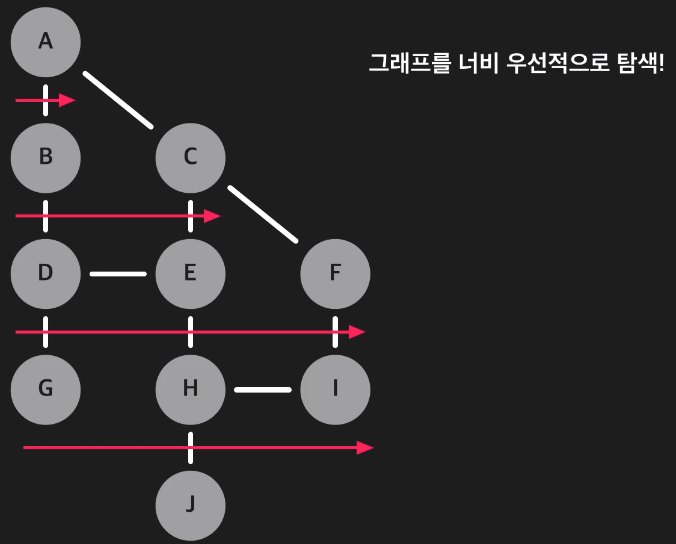
높이, 깊이와는 반대말인 너비를 우선적으로 탐색한다는 말은 위와 같이 그래프의 노드들을 너비(가로) 우선으로 탐색한다는 의미이다.

A를 기준으로

A와 인접한 노드를 찾고 탐색 마침을 표기하고

방금 탐색한 B와 C 노드들에 인접한 노드들을 찾고 탐색 마침을 표기하고 이런 과정을 반복한다.

(이때 탐색한 노드들은 다시 탐색하지 않아도 된다)

이처럼 시작점에서 가까운 노드들을 먼저 탐색한다. 그래프로 보았을 때 수직이 아닌 수평적, 즉 너비를 우선으로 탐색하기 때문에 너비 우선 탐색 알고리즘이라 부른다.

---

BFS 구현하기

BFS 알고리즘을 규현하기 위해선 추상 자료형 큐의 역할이 중요하다

큐는 맨 뒤 데이터 삽입/ 맨 앞 데이터 삭제 및 접근 등을 효율적으로 할 수 있는 추상 자료형으로 아래 포스팅을 참고 좋다.(추상 자료형_1(Python) :: muntari Log (tistory.com))

BFS 알고리즘을 아래와 같이 일반화할 수 있다.

1. 시작 노드(A)를 방문 표시 후, 큐에 삽입한다.

2. 큐에 아무 노드가 없을때까지 아래 명령을 반복한다.

    - 큐의 가장 앞 노드(A)를 추출한다.

    - 추출한 노드(A)를 활용하여 해당 노드(A)에 인접한 노드들(B, C, D...)을 탐색한다.

         - 처음 탐색(방문)하지 않았던 노드(B)라면

              - 탐색(방문) 표시를 해준다.

              - 노드(B) 를 큐에 넣어준다.

        - 한번 탐색을 했던 노드일 경우 위 과정을 건너뛴다.

class StationNode:
    """지하철 역을 나타내는 역"""
    def __init__(self, station_name):
        self.station_name = station_name
        self.adjacent_stations = []
        self.visited = False
        
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ

from collections import deque
from subway_graph import create_station_graph

def bfs(graph, start_node):
    """시작 노드에서 bfs를 실행하는 함수"""
    # 이 함수의 결과로 주어진 노드(탐색기준)과 인접해있는 노드들은 방문표시가 True로 변경되며
    # True로 변경됨은 주어진 노드와 연결(경로)되어있는다는 의미이다.
    queue = deque()  # 빈 큐 생성

    # 탐색을 한번만하지 않기에, 일단 모든 노드를 방문하지 않은 노드로 표시
    for station_node in graph.values():
        station_node.visited = False
    
    # 시작점 노드를 방문 표시 해줌
    start_node.visited = True
     # 큐에 시작점 노드를 넣은 후 반복문 시작
    queue.append(start_node)
    
    # 큐에 노드가 없을때까지 반복
    while queue:
        # 큐의 맨앞 데이터 추출
        queue_frist_node = queue.popleft()

        # 맨앞 추출한 데이터(여기선 노드) 를 이용해 
        # 추출한 노드의 인접해있는 노드들을 돌면서 방문 여부를 변경함
        # 만약 방문하지 않은(false)일 경우 큐에 넣고 큐에 노드가 없을때까지 반반복
        for adjacent_node in queue_frist_node.adjacent_stations:
            if not adjacent_node.visited:
                adjacent_node.visited = True
                queue.append(adjacent_node)


stations = create_station_graph("./new_stations.txt")  # stations.txt 파일로 그래프를 만든다

# stations 딕셔너리의 키 = 강남과 일치하는 value, 즉 station_node를 저장
gangnam_station = stations["강남"]

# 강남역과 경로를 통해 연결된 모든 노드를 탐색
bfs(stations, gangnam_station)

# 강남역과 서울 지하철 역들이 연결됐는지 확인
print(stations["강동구청"].visited)
print(stations["평촌"].visited)
print(stations["송도"].visited)
print(stations["개화산"].visited)

# 강남역과 대전 지하철 역들이 연결됐는지 확인
print(stations["반석"].visited)
print(stations["지족"].visited)
print(stations["노은"].visited)
print(stations["(대전)신흥"].visited)

그래프는 인접 리스트를 이용해 구현하였으며, 자세하 코드는 아래를 참고하면 이해가 더 빠를 것이다.

Python_Javascript_CTEST/use_BFS_search.py at main · Muntari29/Python_Javascript_CTEST (github.com)

---

BFS 시간 복잡도

- 노드 전처리

모든 노드를 방문하지 않은 노드로 표시해주는 로직이 있다.

노드를 항상 생성할 때 False가 디폴트이긴 하나, 탐색을 한 번이라도 진행할 경우 주어진 노드에 인접 관계에 따라 인접된 노드들의 visited 변수가 True로 바뀌는 경우가 있기에 모든 노드를 탐색하지 않은 노드로 만들어 주는 과정이 필요하다.

이때 노드의 수가 V라 할 경우

모든 노드를 다 돌면서 변수 초기화를 해야 하기 때문에 O(V)가 걸린다.

 

- 큐에 노드를 삽입하고 삭제하는 시간

BFS에서는 방문한 노드를 표시하고 다시는 방문하지 않는다.

이 의미는 각 노드는 딱 1번만 큐에 들어가고 다시 들어갈 수 없음을 의미한다. 큐는 더블리 링크드 리스트로 구현이 되어있기에 (python deque) 로직만 보았을 때는 삽입하고 삭제하는 데는 O(1)이 걸리지만

노드의 수가 V라 할 경우

최대 V개의 노드가 큐에 삽입하고 삭제된다.(큐에 들어갔다가 나온다) 때문에 O(1 * V)

O(V)라고 할 수 있다.

 

- 큐에서 추출한 노드의 인접 노드들을 반복하는 시간

인접 리스트에서 한 노드의 연결된 모든 노드를 확인하는 데에는 O(E)가 걸린다.

위에서 BFS에서는 방문한 노드를 다시 방문하지 않음을 알아보았다.

이 말은 각 노드는 딱 1번만 큐에 삽입되고, 삭제될 수 있는데

삭제는 추출이다.

결국 추출은 1번만 가능하고 추출된 노드가 1번 나올 때마다 그 노드의 인접 리스트를 돈다.

이는 모든 노드들의 인접리스트를 딱 1번만 돈다고 할 수 있으며, 

총에지의 수가 E일 경우 E이 비례한 만큼 실행된다고 볼 수 있다.

특정 노드의 인접 리스트가 2개이면 2번 반복하고, 5개면 5번 반복하는 것이다.

따라서, 큐에서 추출한 노드들의 인접 노드들을 반복하는 시간은 총 O(E)라고 할 수 있다.

 

총 시간 복잡도는 O(V) + O(V) + O(E) 

O(2V + E) => O(V + E)이다.

---

DFS

그래프에서 깊이를 우선적으로 탐색한다는 말은 무엇일까?

아래 예시로 알아보자.

BFS 예시와는 다르게 0, 1, 2를 이용해 표기를 사용한다.

방문하지 않은 노드 : 0 , 스택에 들어 있는 노드 : 1, 방문 완료한 노드 : 2

 

---

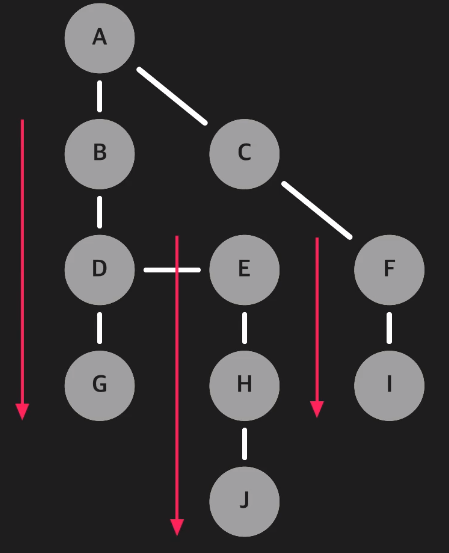
위의 예시에서는 순회 순서를 A => C => B 순으로 하였다.

여기서 주의할 점은 BFS, DFS 모두 A의 인접 노드로 B와 C가 있을 때 B와 C의 순서는 중요하지 않다는 점이다.

이는 인접 리스트에서도 나타나는 특징으로 리스트를 사용하긴 하지만 인접 리스트에서의 노드 들의 순서는 큰 의미가 없다. 모두 동등한 관계(위치)에 있기 때문이다.

---

A를 기준으로

A를 표기 후 스택에 넣는다.

스택에서 가장 맨뒤 데이터를 삭제(추출)하고 추출한 노드의 표기를 방문 완료로 변경해준다.

추출한 노드의 인접한 노드들을 찾으며 표기를 바꾸고 스택에 넣어주며 이 과정을 반복한다.

(이때 탐색한 노드들은 다시 탐색하지 않아도 된다)

깊이 우선 탐색은 말 그대로 깊이를 우선적으로 탐색하는 방법이다.

하나의 노드에 인접한 모든 노드를 우선적으로 탐색하는 (BFS)와 달리

하나의 노드에서 시작해서 최대한 깊이 그리고 멀리 가는 탐색하는 방법을 깊이 우선 탐색 알고리즘이라 부른다.

---

DFS 구현하기

DFS 알고리즘을 규현 하기 위해선 추상 자료형 스택의 역할이 중요하다

스택은 맨 뒤 데이터 삽입/ 맨 뒤 데이터 삭제 및 접근 등을 효율적으로 할 수 있는 추상 자료형으로 아래 포스팅을 참고하면 좋다.(추상 자료형_1(Python) :: muntari Log (tistory.com))

DFS 알고리즘을 아래와 같이 일반화할 수 있다.

1. 시작 노드(A)를 옅은 회색(1) 표기 후, 스택에 삽입한다.

2. 스택에 아무 노드가 없을 때까지 아래 명령을 반복한다.

    - 스택의 가장 맨 뒤 노드(A)를 추출한다.

    - 추출한 노드를 진한 회색(2) 표기한다.

    - 추출한 노드(A)를 활용하여 해당 노드(A)에 인접한 노드들(B, C, D...)을 탐색한다.

         - 처음 탐색(방문) 하지 않았던 노드(0)이라면

              - 탐색(방문)의 옅은 회색(1) 표시해준다.

              - 노드(B)를 스택에 넣어준다.

        - 한번 탐색을 했던 노드일 경우 위 과정을 건너뛴다.

예시를 위해 visited = 0으로  0, 1, 2의 값을 가질 수 있는 인스턴스로 사용하였다.
오로지 예시로 인한 수정 사항으로 BFS에서와 마찬가지로 T/F로 충분히 나타 낼 수 있다.

class StationNode:
    """간단한 지하철 역 노드 클래스"""
    def __init__(self, station_name):
        self.station_name = station_name
        self.visited = 0  # 한 번도 본적 없을 때: 0, 스택에 있을 때: 1, 발견된 상태: 2
        self.adjacent_stations = []

ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
# 예시를 위해 visited = 0으로  0, 1 , 2의 값을 가질 수 있는 인스턴스로 사용하였다.
# 오로지 예시로 인한 수정 사항으로 BFS에서와 마찬가지로 T/F로 충분히 나타 낼 수 있다.

from collections import deque
from subway_graph import *

def dfs(graph, start_node):
    """dfs 함수"""
    stack = deque()  # 빈 스택 생성

    # 모든 노드를 처음 보는 노드로 초기화
    for station_node in graph.values():
        station_node.visited = 0

    # 문제 예시의 편의를 위한것으로 BFS와 마찬가지로 True/False로도 나타낼 수 있다.
    # BFS와 DFS의 가장 큰 차이는 큐/스택 추상 자료형을 이용해 구현한다는 것이다.
    
    # 옅은 회색 표시 후, 스택에 넣어준다.
    start_node.visited = 1
    stack.append(start_node)
    
    # 스택이 빌때까지 반복
    while stack:
        # 스택의 맨 뒤 데이터 삭제(추출)
        stack_last_node = stack.pop()
        # 노드를 추출해오며 해당 노드에 방문 표시를 해준다.
        stack_last_node.visited = 2
        
        # 추출한 노드의 인접 리스트를 돌며
        # 방문하지 않은 노드(0) 일 경우 옅은 회색 표시와 함께 스택에 넣어준다.
        for neighbor_node in stack_last_node.adjacent_stations:
            if neighbor_node.visited == 0:
                neighbor_node.visited = 1
                stack.append(neighbor_node)

stations = create_station_graph("./new_stations.txt")  # stations.txt 파일로 그래프를 만든다

gangnam_station = stations["강남"]

# 강남역과 경로를 통해 연결된 모든 노드를 탐색
dfs(stations, gangnam_station)

# 강남역과 서울 지하철 역들 연결됐는지 확인
print(stations["강동구청"].visited)
print(stations["평촌"].visited)
print(stations["송도"].visited)
print(stations["개화산"].visited)

# 강남역과 대전 지하철 역들 연결됐는지 확인
print(stations["반석"].visited)
print(stations["지족"].visited)
print(stations["노은"].visited)
print(stations["(대전)신흥"].visited)

그래프는 인접 리스트를 이용해 구현하였으며, 자세하 코드는 아래를 참고하면 이해가 더 빠를 것이다.

Python_Javascript_CTEST/use_DFS_search.py at main · Muntari29/Python_Javascript_CTEST (github.com)

---

DFS 시간 복잡도

- 노드 전처리

모든 노드의 visited 초기화에 따른

O(V)

- 스택에 노드를 삽입하고 삭제하는 시간

DFS에서도 스택에 각 노드는 딱 1번만 스택에 들어가고 다시 나올 수 있다.

스택은 더블리 링크드 리스트로 구현이 되어있기에 (python deque) 로직만 보았을 때는 삽입하고 삭제하는 데는 O(1)이 걸리지만

노드의 수가 V라 할 경우

최대 V개의 노드가 스택에 삽입하고 삭제된다. 때문에 O(1 * V)

O(V)라고 할 수 있다.

 

- 스택에서 추출한 노드의 인접 노드들을 반복하는 시간

결국 추출은 1번만 가능하고 추출된 노드가 1번 나올 때마다 그 노드의 인접 리스트를 돈다.

이는 모든 노드들의 인접리스트를 딱 1번만 돈다고 할 수 있으며, 

BFS에서 처럼  O(E)이다.

 

총 시간 복잡도는 O(V) + O(V) + O(E) 

O(2V + E) => O(V + E)이다.

---

BFS/ DFS 시간복잡도

O(V + E)

 

출처 : 코드 잇(자료구조)

자료 구조 | 코드 잇 (codeit.kr)