그래프_최단경로(BFS, Dijkstra)

최단 경로 (Shortest Path)

두 노드 사이에 존재할 수 있는 모든 경로 중 거리가 가장 짧은 경로를 말한다.

비가중치 그래프에서는 경로 중 엣지의 수가 가장 적은 것이 최단 경로이며

가중치 그래프에서는 보통 엣지의 가중치의 합이 가장 적은 경로가 최단 경로가 된다.

---

최단 경로 알고리즘

주어진 그래프에서 두 노드 사이에 가장 짧은 경로를 구하는 방법을 최단 경로 알고리즘이라 부른다.

이 최단 경로 알고리즘은 단 하나의 방법으로 구성되어 있지 않고 여러 방법이 존재한다.

엣지의 방향이 있는지, 가중치가 있는지, 음수 엣지가 존재하는지, 싸이클이 존재하는 지 등등 다양한 그래프 특징에 ㅏ따라 많은 방법이 존재한다.

대표적으로 두 개의 최단 경로 알고리즘인 BFS와 Dijksatr 알고리즘을 알아보자.

1. BFS

=> 비가중치 그래프에서 사용

2. Dijkstar

=> 가중치 그래프에서 사용

---

BFS_최단 경로 알고리즘

이전 포스팅에서 보았던 BFS 너비 우선 탐색 알고리즘에서 하나의 변수를 추가함으로써 구현 할 수 있다.

각 노드를 방문(탐색) 한적이 있는지 없는지에 대해서는 Visited 변수를 사용하였었다.

여기에 더해 predecessor라는 변수를 노드의 인스턴스로 추가해 사용하면 된다.

predecessor는 ~ 이전에 온것 이라는 의미로 BFS에서는 특정 노드에 오기 직전의 노드를 뜻한다.

A에서 인접한 B, C 노드를 방문할때 B와 C는 A를 통해서 방문하였기에

B와 C의 predecessor 변수에 A를 저장하는 방식이다. 

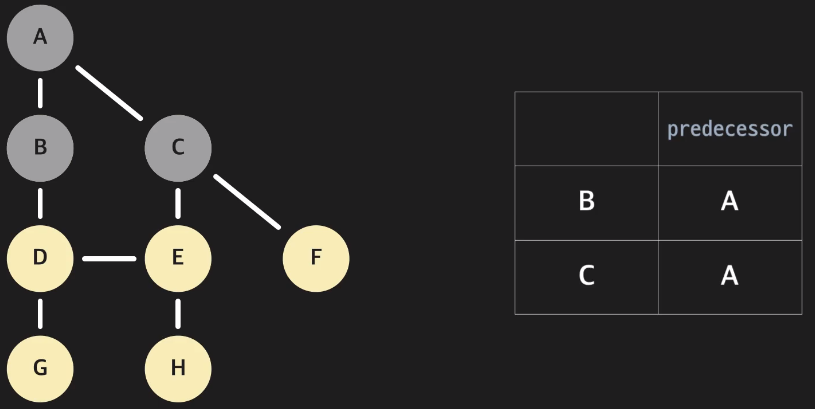
아래와 같이

각 노드의 predecessor를 저장해주면 BFS 알고리즘을 종료한 후

각 노드에 저장되어있는 predecessor 변수를 통해서 최단 경로를 구할 수 있다.

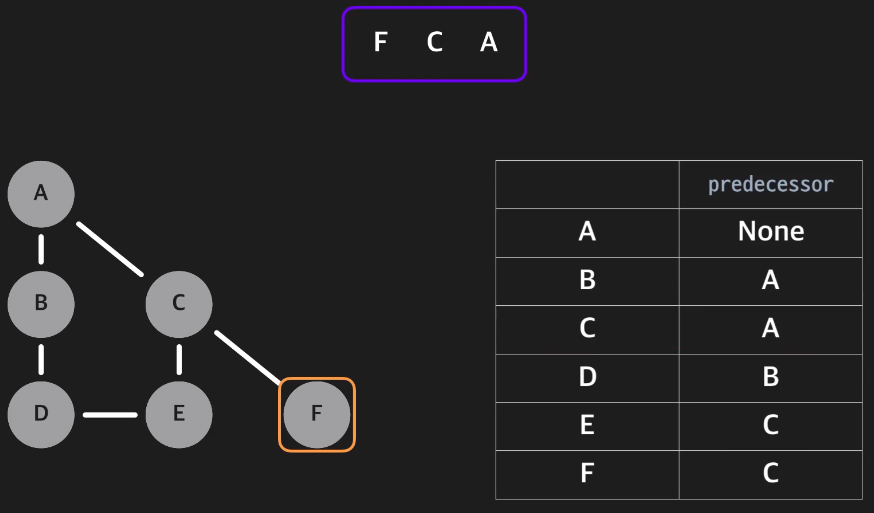
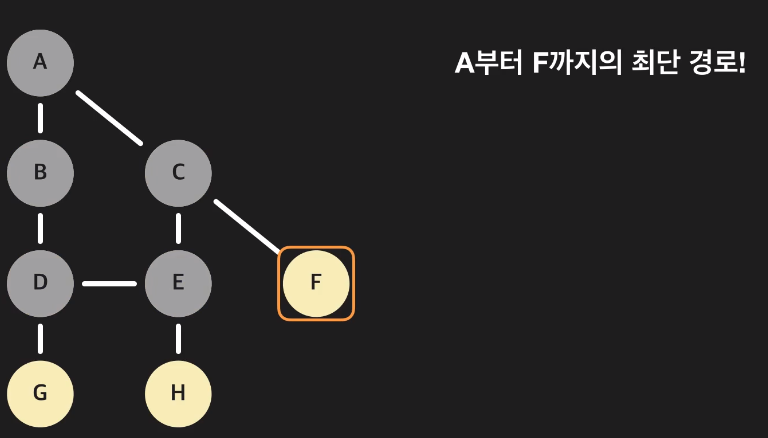
A 에서 F까지의 최단 경로를 구한다고 가정하였을때

F노드의 predecessor 변수로 C노드

C노드의 predecessor 변수로 A노드

A노드의 predecessor 변수는 None으로

F - C - A 해당 값을 거꾸로 뒤집어주면 A - C - F와 같이 A 에서 F까지의 최단 경로를 구할 수 있다.

이렇게 도착점부터 시작점까지 거꾸로 찾아는 것을 Backtracking이라 부른다.

---

BFS_최단 경로 알고리즘 일반화

- 시작 노들르 방문 표시 후, 큐에 넣음

- 큐에 아무 노드가 없을때까지 반복

    - 큐의 가장 앞 노드를 추출

    - 꺼낸 노드에 인접한 노드들을 반복

        - 처음 방문한 노드일 경우

            - 방문 노드 표시 

            - predecessor 변수를 큐에서 꺼낸 노드로 설정

            - 큐에 넣는다.

---

최단 경로의 증명

찾은 경로가 최단 경로라는 것을 증명해보자.

BFS에서는 아래와 같이 노드를 탐색하는 순서에 대한 이해가 먼저 필요하다. (이전 포스팅 참고)

 

아래와 같이

시작 노드와의 거리가 1인 노드를 모두 방문한 후

거리가 2인 노드를 모두 방문하고

거리가 3인 노드를 모두 방문한다.

 

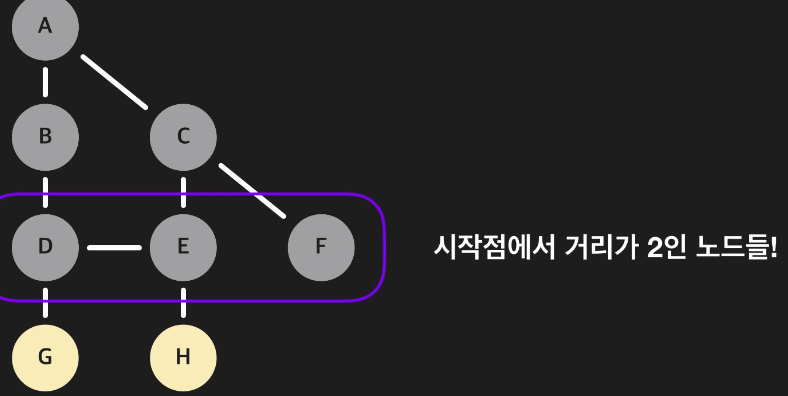
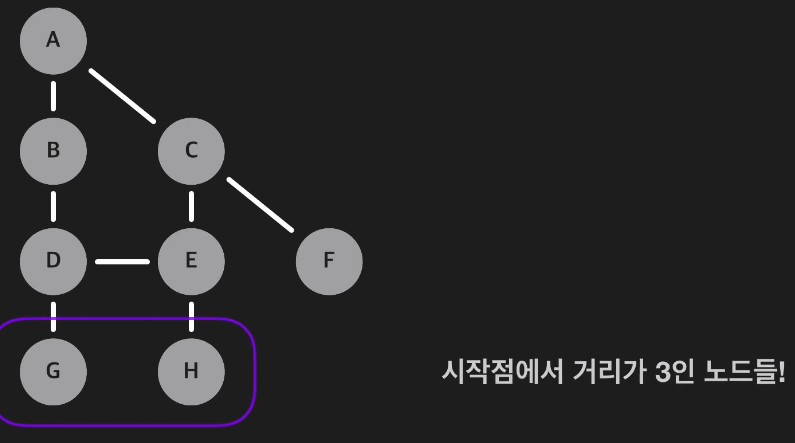
A에서 시작해 F를 처음으로 방문하는 시점이 있을 것이다.

이때는 이미 거리가 1인 노드들은 모두 방문한 후 거리가 2인 노드들을 탐색하고 있다.

만약 A에서 F까지의 거리가 1이라면 F는 거리가 1인 노드들을 탐색할때 이미 찾았을 것이다.

거리가 2인 노드를 탐색했을때 찾았다는 의미는 A에서 F까지의 최단 거리가 2일 수밖에 없다는 의미이다.

F를 처음 탐색하였을때 F까지의 경로를 저장해 높으면 최단 경로를 구할 수 있는 것이며 이것을 predecessor 변수로 이용하는 것이다.

 

F가 가장 빨리 발견되는 경로는 predecessor 변수 C를 통해서이며

C가 가장 빨리 발견되는 경로는 predecessor 변수 A를 통해서이다.

A의 predecessor 변수는 None이므로 이때 알고리즘은 종료된다.

predecessor 변수를 통해 각 노드는 어떤 노드를 통해서 오는게 가장 빠른 지를 저장하고 있다.

비가중치 그래프에서 BFS의 predecessor 변수를 통해 찾은 경로는 최단 경로라 할 수 있다.

---

Dijkstra 알고리즘

가중치 그래프에서 최단 경로를 찾을 수 있는 알고리즘이다.

Dijkstra 를 사용하기 위해서는 그래프 노드의 3가지 변수를 저장해야 한다.

1. distance 

시작점에서 해당 노드까지의 거리를 저장하는 변수

2. predecessor 

현재까지 찾은 최단 경로에서 특정 노드의 직전 노드를 저장하는 변수

3. complete

특정 노드를 완전히 파악했는지 표시하기 위한 변수

---

distance 

최단 거리 예상치

노드를 한번에 모두 방문하는것이 아닌 하나의 노드를 각각 방문하기 때문에 특정 노드를 방문한 시점까지의 최단 거리이다.

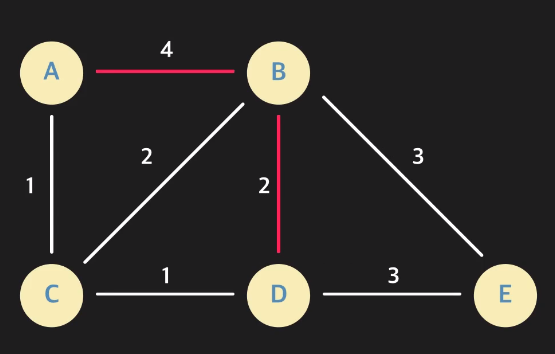
만약 A - B - D로 의 경로를 탐색한 상태(시점)에서는 현재까지 A - C - D 의 경로를 탐색하지 않은 상태이다.

따라서 distance 변수에는 4 + 2 = 6을 저장하고 후에 알고리즘을 진행하며 A - C - D 경로

즉, D로 오는 더 짧은 경로를 찾은 시점에서 distance 변수를 1 + 1 = 2로 수정해 사용한다.

distance 변수는 알고리즘을 진행하며 6, 2 등 더 짧은 경로를 찾을때마다 값을 수정해 사용한다.

 

predecessor 

현재까지 찾은 최단 경로에서 특정 노드의 직전 노드를 저장하는 변수이다.

위에서와 마찬가지로 A - B - D 경로를 찾은 상태이고 A - C - D를 찾지 못한 상태이다.

이때 D의 predecessor 는 직전 노드 B를 저장한다.

알고리즘을 진행하며 D로 오는 더 짧은 경로 A - C - D를 찾으면 predecessor 변수를 C노드로 수정해서 사용한다.

 

complete

특정 노드를 완전히 파악했는지 표시해두기 위한 목적으로 사용하는 변수이다.

초기값은 False이다.

특정 노드를 탐색하고 그 노트까지 가는 경로를 찾았다고 했을때 해당 경로가 최단 경로라 단언할 수 없다.

따라서, 특정 노드에 대한 확실한 최단 경로를 찾았다면 complete 변수를 True로 변경하여 특정 노드를 완전히 파악했다는 표시로 사용하는 것이다.

 

---

엣지 Relaxtion

Dijkstra 알고리즘에서는 노드를 하나씩 방문(탐색)한다.

노드들을 방문하면서 해당 노드의 distance와 predecessor 변수를 계속 갱신하며 알고리즘을 진행하는데

이렇게 2가지 변수를 갱신하는 것을 Relaxtion, relax라고 표현한다.

A에서 B를 방문할 때 B에 변수를 갱신하는 것을

엣지 (A, B)를 relax한다 라는 표현한다.

 

아래의 예시로 엣지 (A, B)를 relax를 이해해보자

A의 distance + 엣지(A, B) 가중치를 더한 값과 B의 distance를 비교한다.

B의 distance가 7이라는 뜻은

현재까지 아는 정보(경로)로는 시작점에서 B의 최단거리가 7이라는 뜻이다.

이때 A의 distance + 엣지(A, B) 가중치를 더한 값 5가 더 작다는 의미는 

시작점에서 B까지 가는 경로 중 7보다 더 짧은 거리를 발견했다는 의미로

B의 distance를 5로 갱신해준 후 + B의 predecessor 룰 A로 갱신한다.

 

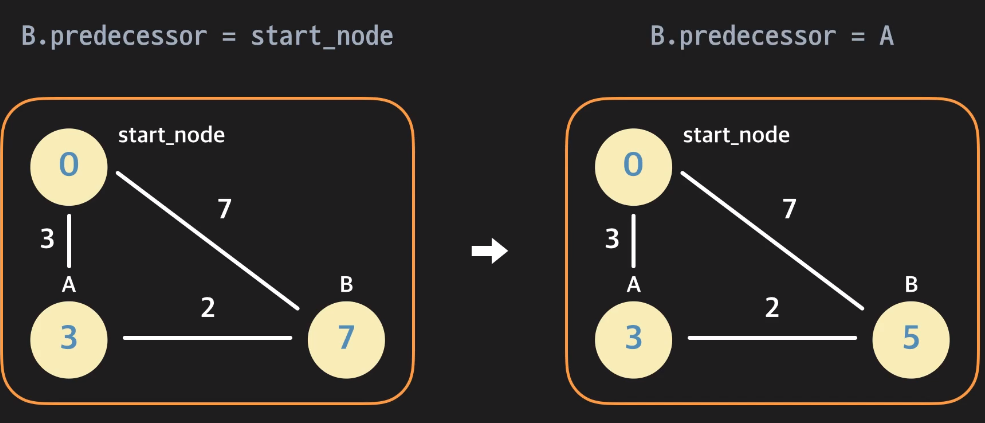
만약 반대로 A의 distance + 엣지(A, B) 가중치를 더한 값이 더 클 경우 아무것도 변경해 주지 않으면 된다.

지금까지 찾은 B의 distance가 최단 경로라는 의미이기 때문이다.

이처럼 A에서 B로 가는 경로의 distance가 현재 B의 distance보다 작은지 확인하고 갱신해 주는 것을 

엣지 (A, B)를 relax 한다고 표현한다.

---

Dijkstra 최단 경로 알고리즘

처음 시작은 방문한 노드가 아무것도 없기에 distance , predecessor, complete(fasle)로 모두 초기화한다.

 

시작점을 시작으로 시작점에서 시작점까지의 경로는

자기 자신으로 거리는 0, predecessor 는 None

이제 complete 처리가 되지 않은 노드 중 가장 작은 distance를 갖는 노드를 본다 (A)

그다음 A의 엣지들을 보며 연결된 엣지의 노드가 complete True인 경우 건너뛴다.

아직까지는 처리된 노드가 하나도 없기 때문에 엣지 (A,B), (A, C)를 relax 해준다.

 

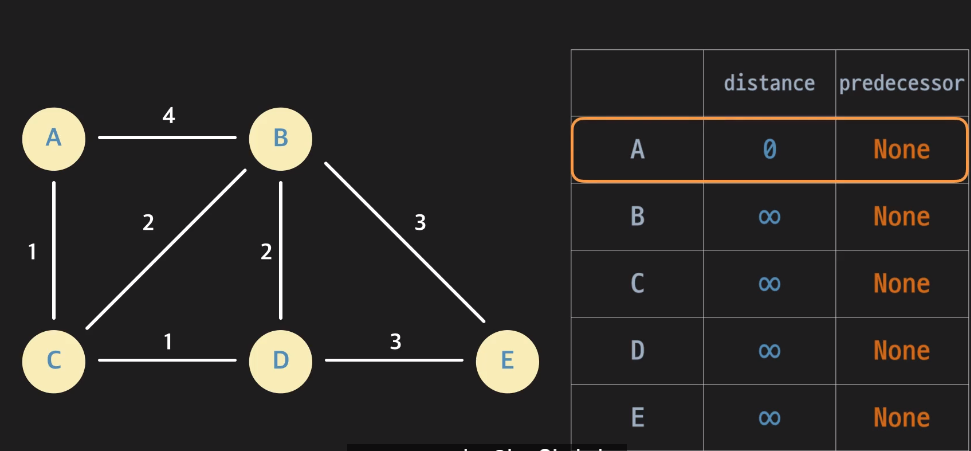
엣지 (A, B), 엣지 (A, C)를 relax해 두 변수를 갱신해준 후 A를 complete 처리한다(True)

이때 엣지(A,B) relax의 결과로 B의 거리는 3으로 갱신된다.

 

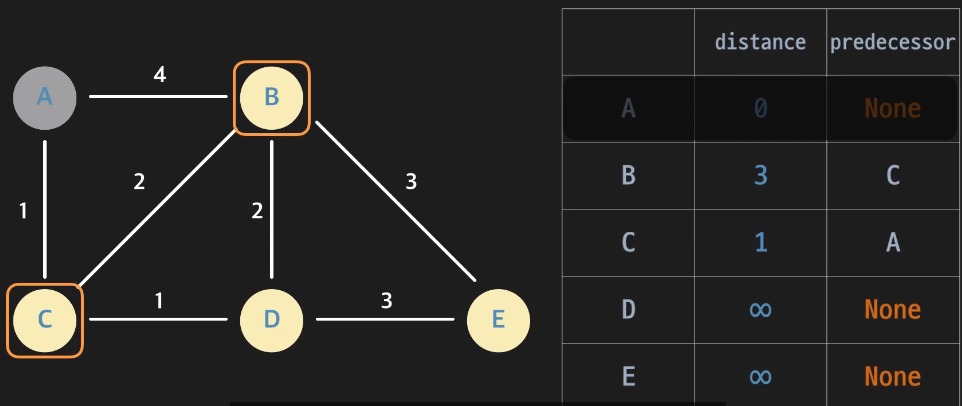
A를 complete처리한 후 이제 complete 처리가 되지 않은 노드 중 가장 작은 distance를 갖는 노드를 본다 (C)

위  과정을 모든 노드가 complete 처리 될까지 반복한다.

 

알고리즘이 종료 되면 모든 노드의 distance와 predecessor 값이 확정되어 저장된 것을 활용 할 수 있다.

만약 시작점으로 부터 최단 거리를 알고 싶다면 distance를

최단 경로를 알고 싶다면 predecessor를 이용해 Backtracking을 하면 된다.

A에서 E의 최단 경로를 알고 싶다면

E노드의 predecessor 변수로 D노드

D노드의 predecessor 변수로 C노드

C노드의 predecessor 변수로 A노드

A노드의 predecessor 변수는 None

E - D - C - A를 뒤집으면 A - C - D - E가 최단 경로라는 의미이며 이때의 최단 거리를 알고싶다면

E의 distance 5를 읽어들이면 된다.

---

Dijkstra 알고리즘 일반화

일반화하여 나타내면 아래와 같다.

- 시작점의 distance를 0, predecessor 를 None

- 모든 노드가 complete일때까지 반복

    - complete 하지 않은 노드 중 distance가 가장 작은 노드를 선택

    - 이 노드에 인접한 노드 중 complete 하지 않은 노드를 반복

        - 각 엣지를 relax

    - 현재 노드를 complete 처리

---

최단 경로의 중요 성질

아래와 같은 예시에서 A 에서 E로 가는 최단 경로를 예시로 최단 경로의 중요 성질을 알아보자.

이때 최단 경로는 A - C - D- E이다.

여기서 부분 경로라는 개념이 나오는데

부분 경로란 간단하게 특정 경로 안에 포함되는 경로로 이해하면 된다.

A - C - D- E에서 A - C- D / C - D - E 같이 특정 경로 안에 포함되어있는 경로를 부분 경로라 부른다.

 

최단 경로가 A - C - D- E 라면

A - C - D = A에서 D로 가는 최단 경로이며

C - D - E = C에서 E로 가는 최단 경로라고 말할 수 있다.

즉, 최단 경로안의 부분 경로들은 모두 최단 경로라는 의미이다.

 

만약 최단 경로가 A - C - D- E 일때

A - B - D = A에서 D로가는 경로라 최단 경로라고 가정하면 애초에 위의 최단 경로 조건이 말이 되지 않는다.

명제 자체가 오류를 범하기에 A - B - D가 최단 경로라면,

해당 경로는 A - C - D -E의 부분 경로가 아니기에 애초에 명제는 A - B - D - E가 되어야 한다.

 

이로 인해 A에서 E까지 최단 경로를 찾는 문제는 A에서 D까지의 최단 경로를 찾는 문제와 연관이 있고, A에서 B까지 찾는 문제 와도 연관이 있고, A에서 C까지의 최단 경로를 찾는 문제와도 연관이 있다고 할 수 있다.

최단 경로를 구하기 위해서 부분 최단 경로를 이용할 수 있다는 이야기이다.

어느 특정 최단 경로를 찾았다면 최단 경로안의 부분 경로안에서는 각각 모두 최단 경로임을 인지하고 활용 할 수 있다는 것이다.

 

참고 : Python_Javascript_CTEST/shortest_path_BFS.py at main · Muntari29/Python_Javascript_CTEST (github.com)

출처 : 코드 잇(자료구조)

자료 구조 | 코드 잇 (codeit.kr)