-
728x90반응형
그래프 구현하기
그래프를 구현하는 방법은 크게 2가지로 나누어 알아보자.
1. 그래프의 노드를 구현하는 방법
- 배열 또는 동적 배열 => 파이썬의 리스트로 구현이 가능하다.
- 해시 테이블 => 파이썬의 딕셔너리로 구현이 가능하다.
2. 그래프의 에지를 구현하는 방법
- 인접 행렬
- 인접 리스트
먼저, 그래프의 노드를 구현하는 방법이다.
1. 동적 배열 / 파이썬 리스트 구현 방법
그래프는 노드라는 기본 데이터 단위를 가지며 리스트의 요소로 단순 값이 아닌 노드 자체를 요소로 하는 리스트를 만드는 방법이다.
이때 노드는 특정 인덱스 값을 부여받는데, 인덱스를 이용해 리스트의 O(1)으로 효율적인 접근이 가능하며, 노드 안의 인스턴스에 대한 접근도 그만큼 효율적으로 할 수 있게 되는 것이다.
class StationNode: """간단한 지하철 역 노드 클래스""" def __init__(self, station_name, location): self.station_name = station_name self.location = location A = StationNode("당고개역", "서울") B = StationNode("오이도역", "경기") C = StationNode("부산역", "부산") list_1 = ["당고개역", "오이도역", "부산역"] list_2 = [A, B, C] print(list_1) print(list_2[1].station_name) # 오이도역 print(list_2[1].location) # 경기
2. 헤시테이블 / 파이썬 딕셔너리 구현 방법
위 방법과 비슷하게 역 이름 자체를 Key 값으로 사용하고 역 노드를 Value 값으로 사용하는 것이다.
이때 주의할점은 해시 테이블에서 동일한 key값은 존재할 수 없다는 점이며, 중복이 이루어지지 않는 고윳값(이메일, 핸드폰 번호 등등)을 Key 값으로 사용해야 한다.
역 이름의 경우 중복되는 역 이름은 존재하지 않으므로 역 이름을 Key 값으로 사용해도 무방하다.
해시 테이블도 Key 값만 있다면 Value는 평균적으로 O(1)으로 가져올 수 있기에 효율적으로 사용이 가능하다.
class StationNode: """간단한 지하철 역 노드 클래스""" def __init__(self, station_name, location): self.station_name = station_name self.location = location A = StationNode("당고개역", "서울") B = StationNode("오이도역", "경기") C = StationNode("부산역", "부산") my_dict = {} my_dict["당고개역"] = A my_dict["오이도역"] = B my_dict["부산역"] = C print(my_dict) # {'당고개역': <__main__.StationNode object at 0x7fdf45868700>, '오이도역': <__main__.StationNode object at 0x7fdf458d4490>, '부산역': <__main__.StationNode object at 0x7fdf458d4520>} print(my_dict["당고개역"].station_name) # 당고개역 print(my_dict["당고개역"].location) # 서울
그래프의 엣지를 구현하는 방법
1. 인접 행렬
인접은 두 노드가 서로 연결되어 있다는 의미이고,
행렬은 2차원 배열 또는 2차원 리스트라는 의미이다, 파이썬에서의 리스트 안에 리스트가 들어가 있는 matrix형태를 떠올리면 되겠다.
즉, 요소의 갯수에 따라 행렬을 만들고 이 행렬에 각 노드들끼리 어떻게 연결되었는지를 표시하는 방법이다.
인접 행렬의 목표는 어떤 노드가 어떤 노드와 연결되어 있는지? 를 확인하기 위함이라 할 수 있겠다.
인접 행렬을 아래와 같이 정리할 수 있다.
- 각 노드를 리스트에 저장해 노드는 고유 정수 인덱스 값을 갖는다.
- 노드 수 X 노드 수 크기의 행렬을 만든다.
- 노드들의 엣지 유무 및 가중치에 따라 행렬의 요소를 채운다.
인접 행렬은 무방향 그래프, 방향 그래프, 가중치 그래프일 때 각각 다르기 때문에 그래프 별로 알아보자.
- 무방향 그래프
아래의 예시로 엣지를 구현해보도록 하자.
list_1 = ["영훈", "동욱", "현승", "지웅", "소원"]
각 노드 간의 연결 관계를 저장하기 위해 노드의 개수만큼의 행렬을 만들어 준다. (5 x 5)
각 노드는 인덱스라는 고유 값을 갖게 되므로 이를 이용해 서로 간의 연결 관계를 정의할 수 있는데
인접 행렬에서는 모든 노드는 스스로와 연결이 되지 않은 상태로 나타낸다. (0)
영훈의 경우 0번째 인덱스로 동욱, 현승과 인접 관계에 있다.
이를 행렬로 나타내면 아래와 같다.

무방향 그래프에서의 영훈 - 동훈 에지는 동훈 - 영훈 에지와 같기 때문에
0행 1열(영훈, 동훈) = 1 / 1행 0열(동훈, 영훈) = 1
0행 2열(영훈, 현승) = 1 / 2행 0열(현승, 영훈) = 1
모든 노드에 위와 같이 관계를 정의해주면 아래와 같은 행렬이 되며,
모든 노드는 스스로와 연결이 되지 않은 상태이기에 대각선을 기준으로 대칭 구조가 된다.

- 방향 그래프
위 예시에 방향성만 추가한다.

방향 그래프에서는 엣지가 방향성을 갖기 때문에 영훈- 현승 에지와 현승 -영훈 에지가 다르다.
0행 1열 (영훈, 현승) = 0 / 1행 0열 (현승, 영훈) = 1
0행 2열 (영훈, 동욱) = 0 / 2행 0열 (동욱, 영훈) = 1
모든 노드에 위와 같이 관계를 정의해주면 아래와 같은 행렬이 되며,
무방향에서와 달리 대칭 구조를 이루지 않는다.

- 가중치 그래프
엣지가 추가 정보를 갖는 가중치 그래프
여기서는 연결 상태 표시를 가중치로 해주면 된다.
위에서 연결 상태 = 1로 표기하였다면 연결 상태 = 가중치로 표기해주면 되는 것이다.
당연히 기본 단위인 노드의 인스턴스는 위 예시와 다르다.

인접 행렬의 목표는 어떤 노드가 어떤 노드와 연결되어 있는지?를 알기 위함이었다.
특정 노드 사이에 서로 인접해 있는지 여부를 확인하는 방법을 알아보자.

영훈과 동욱이 서로 인접해 있는지 확인하기 위해서는
영훈의 인덱스 값 0과 동욱의 인덱스 값 1을 이용해 행렬의 데이터를 찾으면 된다.
즉, 0행 1열의 값 또는 1행 0열의 값을 찾아 서로 인접해 있는지 아닌지 여부를 확인할 수 있다.
matrix[0][1] or matrix[1][0]
특정 노드와 인접해 있는 모든 노드를 확인하고 싶을 때는 특정 노드의 인덱스 값을 이용해 해당 노드의 행 전체를 가져오면 된다.
영훈과 인접해 있는 모든 노드를 확인하고 싶을 때는 아래와 같이 확인할 수 있으며
결과로 동욱, 현승과 인접 관계라는 점을 확인 할 수 있게 된다.
matrix[0]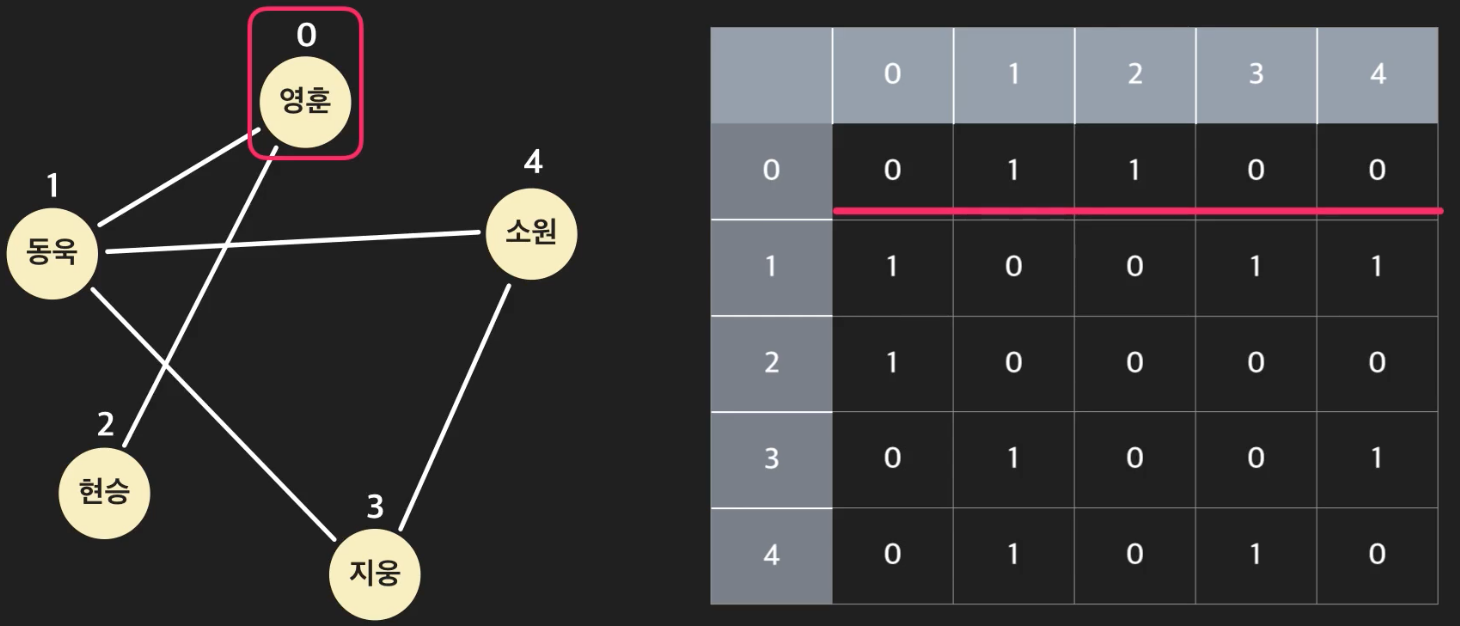
2. 인접 리스트
인접 행렬의 경우 노드들의 인접 데이터를 행렬에 저장했다면,
인접 리스트의 경우, 말그대로 노드들의 인접 데이터를 리스트에 저장하는 방법이다.
(리스트는 순서 데이터를 저장하는 자료구조이나, 인접 리스트에서는 노드들의 순서는 큰 의미가 없다. 모두 동등한 관계이자 위치에 있기 때문이다.)
인접 리스트는 각 노드마다 스스로 인접한 노드들에 대한 레퍼런스를 리스트로 저장하여 에지를 구현하는 방법이다.
인접 행렬을 아래와 같이 정리할 수 있다.
- 각 노드의 엣지를 리스트에 저장하는 방법.
아래 지하철 역 예시를 통해 더 자세히 알아보자.
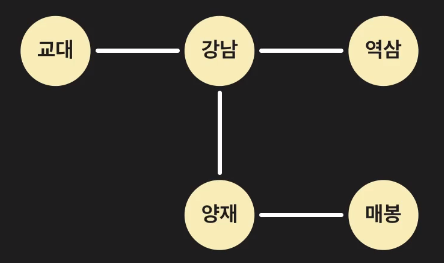
강남역의 경우
교대, 역삼, 양재와 인접해있으며, 이 인접 관계를 배열 or 파이썬의 리스트에 저장하는 방법으로
특정 노드에 어떤 노드들이 인접해 있는지 알 수 있게 된다.

인접 행렬에서의 노드 인스턴스에 빈 배열의 인스턴스를 추가하고
이 빈 배열에 연결된 노드들에 대한 레퍼런스를 저장한다!
(이는, 링크드 리스트의 노드에서 다음 노드에 대한 레퍼런스를 저장하는 것과 트리에서 노드가 자식 노드에 대한 레퍼런스를 저장하는 것과 동일하다!!)
class StationNode: """간단한 지하철 역 노드 클래스""" def __init__(self, station_name, location): self.station_name = station_name self.location = location self.adjacent_stations = []따라서 그래프의 강남 노드는 아래와 같은 인접 리스트를 갖는다!

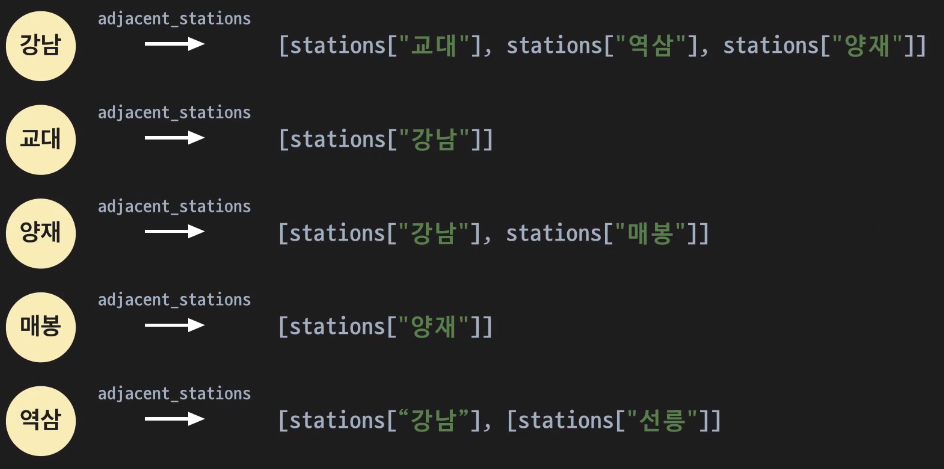
인접 리스트를 사용하는 방법
그래프에 따라 인접 리스트를 사용하는 방법에 차이가 있다.
1. 무방향 그래프
A와 B가 인접 관계라면 A의 인접 리스트에 B를 넣고 + B의 인접 리스트에 A를 넣는다.
에지의 방향성이 없기에 A - B 에지와 B - A 에지는 같기 때문이다.

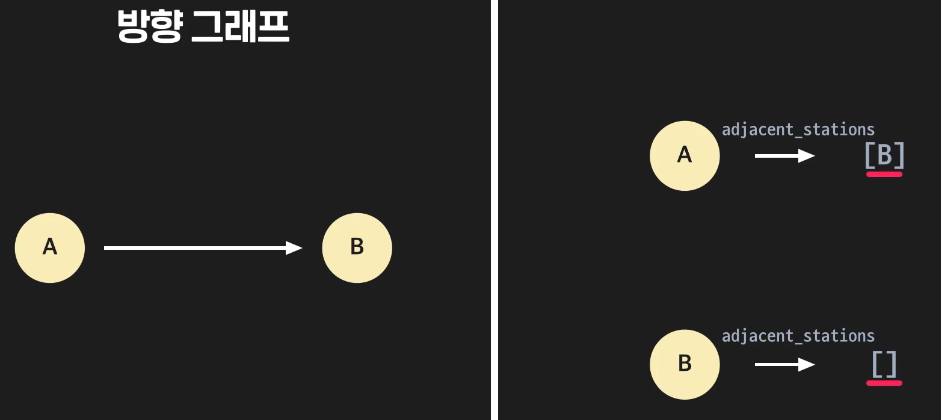
2. 방향 그래프
A와 B가 인접 관계라면 A의 인접 리스트에 B를 넣고, B의 인접 리스트에 A를 넣지 않는다.
엣지의 방향성이 있어, A - B 에지와 B - A 에지는 같지 않기 때문이다.
3. 가중치 그래프
가중치 그래프의 경우 튜플을 사용하여 인접 노드와 가중치를 함께 저장해주면 된다.
만약, 가중치 그래프에서 에지의 방향성이 있다면 위와 마찬가지로 B의 인접 리스트에 A를 넣지 않으면 된다.

그래프는 각 언어별로 아래와 같은 방법으로 구현한다고 한다.
C++ => Vector
JAVA => Arraylist
Python => List
구현의 경우 여태껏 구현하였던 자료구조 중 제일 복잡하였덧 것 같아 코드를 참고하여 공부한다면 더 잘 이해가 될 것 같아 공유한다!
출처 : 코드 잇(자료구조)
728x90반응형