-
그리디_체육복_Python카테고리 없음 2021. 6. 17. 14:59728x90반응형
문제 설명
점심시간에 도둑이 들어, 일부 학생이 체육복을 도난당했습니다. 다행히 여벌 체육복이 있는 학생이 이들에게 체육복을 빌려주려 합니다. 학생들의 번호는 체격 순으로 매겨져 있어, 바로 앞번호의 학생이나 바로 뒷번호의 학생에게만 체육복을 빌려줄 수 있습니다. 예를 들어, 4번 학생은 3번 학생이나 5번 학생에게만 체육복을 빌려줄 수 있습니다. 체육복이 없으면 수업을 들을 수 없기 때문에 체육복을 적절히 빌려 최대한 많은 학생이 체육수업을 들어야 합니다.
전체 학생의 수 n, 체육복을 도난당한 학생들의 번호가 담긴 배열 lost, 여벌의 체육복을 가져온 학생들의 번호가 담긴 배열 reserve가 매개변수로 주어질 때, 체육수업을 들을 수 있는 학생의 최댓값을 return 하도록 solution 함수를 작성해주세요.
제한사항
- 전체 학생의 수는 2명 이상 30명 이하입니
- 다.
- 체육복을 도난당한 학생의 수는 1명 이상 n명 이하이고 중복되는 번호는 없습니다.
- 여벌의 체육복을 가져온 학생의 수는 1명 이상 n명 이하이고 중복되는 번호는 없습니다.
- 여벌 체육복이 있는 학생만 다른 학생에게 체육복을 빌려줄 수 있습니다.
- 여벌 체육복을 가져온 학생이 체육복을 도난당했을 수 있습니다. 이때 이 학생은 체육복을 하나만 도난당했다고 가정하며, 남은 체육복이 하나이기에 다른 학생에게는 체육복을 빌려줄 수 없습니다.
입출력 예
nlostreservereturn
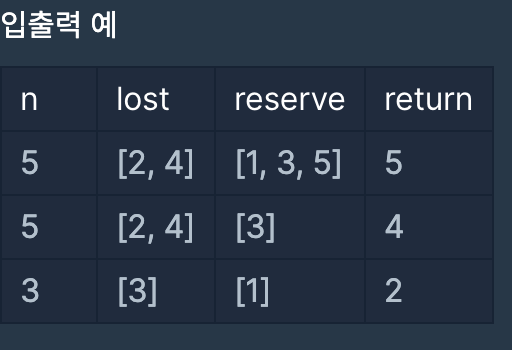
입출력 예 설명
예제 #1
1번 학생이 2번 학생에게 체육복을 빌려주고, 3번 학생이나 5번 학생이 4번 학생에게 체육복을 빌려주면 학생 5명이 체육수업을 들을 수 있습니다.예제 #2
3번 학생이 2번 학생이나 4번 학생에게 체육복을 빌려주면 학생 4명이 체육수업을 들을 수 있습니다.
접근 방법
그리디 알고리즘이란 매 순간 순간 마다 최선의 선택을 하는 기법이다.
하나의 큰 문제를 해결하기 위해 부분 문제를 해결하는 방법으로 분할 정복과 비슷하긴 하지만
순간 순간의 선택이 최선이길 바라는 알고리즘이다.
그렇기에 순간 순간 답을 찾을 순 있지만 큰 문제를 반드시 해결 할 수 있다는 보장은 없다.
따라서, 가장 좋은 해법이 될 수도 있고, 아닐 수도 있다.
허나 그리디 알고리즘으로 간단하고 쉽게 풀리는 문제들도 많이 존재한다.
말 그대로 문제를 해석하고 푸는 방법을 하나하나 순차적으로 해결해 나가는 것이라도 할 수 있을 것같다.
그리디를 몰랐지만, 그리디를 항상 적용해 오던 것이다.
아래 코드의 주석을 참고하면 될 것 같다.
def solution(n, lost, reserve): # 학생 수 만큼의 리스트 생성 answer = 0 stu_list = [student for student in range(1, n+1)] # [1, 2, 3, 4, 5] # [1, 2, 3] # 도난 당한 학생번호를 0으로 갱신 # 이때 도난 당한 학생이 여분을 갖고 있는 학생일 경우를 포함 for a in lost: if a in reserve: continue stu_list[a - 1] = 0 for i in range(len(stu_list)): front = 0 back = 0 case = 0 # 도난 당한 학생이 여분이 있는 학생인 경우 if stu_list[i] == 0: # 도난 당한 학생번호가 맨 앞 if i == 0 : case = 1 back = stu_list[i+1] # 도난 당한 학생번호가 맨 뒤 elif i == len(stu_list) - 1: case = 2 front = stu_list[i-1] # 도난 당한 학생번호가 중간에 위치할 경우 else: case = 3 froun = stu_list[i-1] back = stu_list[i+1] # 도난 당한 학생 앞 뒤에 여분을 가져온 학생이 있는 경우 if case == 1: if back in reserve: # i =0 stu_list[i] = i+1 elif case == 2: if front in reserve: # i == 5 stu_list[i] = i+1 elif case == 3: if front in reserve or back in reserve: stu_list[i] = i +1 print(stu_list) for i in stu_list: if i != 0: answer +=1 return answer
개선_2
# 도난 당한 학생번호를 0으로 갱신하는 로직에 remove로 도난 당한 학생이 여분을 가지고 있는 학생일 경우를 추가해줬다.
정확도가 높아지긴 했으나 아직도 문제가 있다.
def solution(n, lost, reserve): # 학생 수 만큼의 리스트 생성 answer = 0 stu_list = [student for student in range(1, n+1)] # [1, 2, 3, 4, 5] # [1, 2, 3] # 도난 당한 학생번호를 0으로 갱신 # 이때 도난 당한 학생이 여분을 갖고 있는 학생일 경우를 포함 for a in lost: if a in reserve: reserve.remove(a) continue stu_list[a - 1] = 0 for i in range(len(stu_list)): front = 0 back = 0 case = 0 # 도난 당한 학생이 여분이 있는 학생인 경우 if stu_list[i] == 0: # 도난 당한 학생번호가 맨 앞 if i == 0 : case = 1 back = stu_list[i+1] # 도난 당한 학생번호가 맨 뒤 elif i == len(stu_list) - 1: case = 2 front = stu_list[i-1] # 도난 당한 학생번호가 중간에 위치할 경우 else: case = 3 froun = stu_list[i-1] back = stu_list[i+1] # 도난 당한 학생 앞 뒤에 여분을 가져온 학생이 있는 경우 if case == 1: if back in reserve: # i =0 stu_list[i] = i+1 elif case == 2: if front in reserve: # i == 5 stu_list[i] = i+1 elif case == 3: if front in reserve or back in reserve: stu_list[i] = i +1 print(stu_list) for i in stu_list: if i != 0: answer +=1 return answer
개선_3
#도난 당한 학생번호가 중간에 위치하는 경우에서
froun 오타발견
오타를 수정하며 로직의 문제점을 확인하여
여분을 가져온 학생은 여분은 반드시 1개만 가지고 온다는 점
- 여벌 체육복을 가져온 학생이 체육복을 도난당했을 수 있습니다. 이때 이 학생은 체육복을 하나만 도난당했다고 가정하며, 남은 체육복이 하나이기에 다른 학생에게는 체육복을 빌려줄 수 없습니다.
즉 누군가를 빌려주면 더이상 빌려줄수 없다.
따라서 reserve 값에서 삭제하는 로직을 추가하였다.
def solution(n, lost, reserve): # 학생 수 만큼의 리스트 생성 answer = 0 stu_list = [student for student in range(1, n+1)] # [1, 2, 3, 4, 5] # 도난 당한 학생번호를 0으로 갱신 # 이때 도난 당한 학생이 여분을 갖고 있는 학생일 경우를 포함 for a in lost: if a in reserve: reserve.remove(a) continue stu_list[a - 1] = 0 # 조건에 맞게 stu_list 갱신 for i in range(len(stu_list)): front = 0 back = 0 case = 0 # 도난 당한 학생(0)일 경우 if stu_list[i] == 0: # 도난 당한 학생번호가 맨 앞 case 1 if i == 0 : case = 1 back = stu_list[i+1] # 도난 당한 학생번호가 맨 뒤 case 2 elif i == len(stu_list) - 1: case = 2 front = stu_list[i-1] # 도난 당한 학생번호가 중간에 위치할 경우 case 3 else: case = 3 front = stu_list[i-1] back = stu_list[i+1] # 도난 당한 학생 바로 뒤, 여분을 가져온 학생이 있는 경우 if case == 1: if back in reserve: # i =0 stu_list[i] = i+1 reserve.remove(back) # 도난 당한 학생 바로 앞, 여분을 가져온 학생이 있는 경우 elif case == 2: if front in reserve: # i == 5 stu_list[i] = i+1 reserve.remove(front) # 도난 당한 학생 양 옆, 여분을 가져온 학생이 있는 경우 elif case == 3: # 여분은 반드시 1개이므로 reserve를 활용후 값 삭제 if front in reserve : stu_list[i] = i +1 reserve.remove(front) elif back in reserve: stu_list[i] = i +1 reserve.remove(back) # 남아있는 stu_list에서 0이 아닌 값들을 카운트한다. for i in stu_list: if i != 0: answer +=1 return answer
다른 사람 참고 답변하여 재 풀이
사실 로직이 너무 길어서 브루트 포스로 문제를 푼것 같다.
해당 문제에서는 여분이 있는 학생이 도난을 당하면 여분을 다른 학생에게 빌려줄 수 없게 된다.
이때 이걸 어떻게 처리할 거냐가 핵심이며
이 문제의 출제 의도는 중복되는 학생들을 어떻게 처리해줄 것이냐가 관건인거 같다.
나처럼 의식의 흐름처럼 작성하는 건 그리디 알고리즘이라 보기 어렵다.
특정 문제에 대한 핵심 조건이나 키워드가 있는데 이를 잘 파악하고 활용할 줄 알아야
이 로직이 최선의 로직이 되겠다는 조건이 성립되지 않나 싶다.
def solution(n, lost, reserve): # 여분이 있는 학생이 도난 당했을 경우 다른 사람에게 빌려줄 수 없게 된다. # 남은 여분을 자기가 입어야하기 때문이다. # 여분이 있는 학생이 도난 당한 학생일 경우를 제외하고 새로운 reserve를 만든다. new_reserve = [new for new in reserve if new not in lost] # 도난 당한 학생이 여분이 있는 학생일 경우를 제외하고 새로운 lost를 만든다. new_lost = [new for new in lost if new not in reserve] # print(new_reserve) # [1, 3, 5] # print(new_lost) # [2, 4] # 여분이 있는 학생을 기준으로 앞, 뒤 학생을 구함 # 이 조건과 반복문을 사용할 수 있는 이유는 학생 번호(int) == 곧 학생이기 때문이다. for i in new_reserve: front = i - 1 back = i + 1 # 여분이 있는 학생의 앞 순서에 있는 학생이 도난 당한 학생일 경우 # 여분을 전달한다는 의미로 해당 학생번호를 도난 당한 학생 리스트에서 삭제한다. if front in new_lost: new_lost.remove(front) # 여분이 있는 학생의 뒤 순서에 있는 학생이 도난 당한 학생일 경우 elif back in new_lost: new_lost.remove(back) return n - len(new_lost)
시간복잡도
나의 풀이도 그렇고 거의 대부분 조건식으로
for문과 remove를 사용한 것을 감안하여
총 시간 복잡도는 O(N^2)
728x90반응형